2021-07-12

1億円を調達したのに、しくじった無能経営者のワイ

株式会社MatrixFlow 代表取締役 tdualです。

調子に乗っているこの記事から色々状況も変わりました。
tdual.hatenablog.com

１番のイベントは、昨年の10月末に初調達でプレシリーズAで1億円の調達をした事です。

1億円あればいろんなことが出来るはずですが、色々ミスったので自戒を込めて記事を残します。

ミス① 動きが遅い

あらゆることにはタイムラグがあります。
いきなり必要な人材の確保は出来ないし、何かの施策をするにも芽吹くには時間がかかります。
弊社は人材の確保は、調達が決まりそうな段階から動き出してまあまあ良かったです。
採用面談は無料なのでバンバンやりました。

問題は、広告宣伝でした。
調達するまで、弊社はあまりマーケティング・営業をちゃんとやってなかったので、
広告宣伝の意義が良くわかっていませんでした。
今だから分かるけど、「じゃあどうやってリードをとってくるの？」って話です。
広告は結構お金が掛かります。でも、営業を効率的に動かすためには必要不可欠です。
なので、資金調達が決まりそうになったら広告宣伝費に突っ込む準備をしましょう。

ミス② 手放せないタスク

もうさっさといろんな事を人に任せるべきでした。
ちょっと複雑で面白くもないタスクなので新しく入った人に任せるのが申し訳なくて自分でやってしまってました。
しかし、このシリーズの経営者の仕事は、組織醸成、PMFのための動き、次の調達の準備です。
調達しても結局ズルズル些細なタスクを背負って上記のことにフルコミット出来てませんでした。
とりあえず、どんなに嫌な仕事でも社員に振るべきです。

ミス③ PMFは簡単じゃない

舐めてました。
一つの企業で使ってもえば、同じ業界で横展開するなんてのは経営者のよくある妄想です。
また、当たり前ですけど、営業の立ち上がりにも時間がかかります。
そもそもPMFってどういう状況なんだよって感じですよね。
逆説的ですけど、それが実感できてない段階でPMFできてないってことなんだと思います。
サービスを売る事の難しさを痛感する日々です。

ミス④ 嫉妬と自己嫌悪

このシリーズになれば、経営者仲間も出来ると思います。
彼、彼女らのfacebookを見てるとキラキラしてて、
無能な自分はなんで停滞してるのに、彼、彼女らはなんて前進してるんだって思います。
しかし、見えてるものは氷山の一角で彼、彼女らも同じ様な苦悩はしてます。（facebookには良い事しかあげないよなぁ！）
また、ビジネスモデルによっても成長のスピードは違うので、他のスタートアップは気にしても仕方ないです。
そんな知り合いの会社を気にしてる暇があるなら、競合を気にしましょう。

おわり

しくじったけど死んではないのでこれからも全力で頑張ります！

経営者仲間との交流も求めているので気軽に連絡ください！！
これから起業する人もワイが出来る範囲でアドバイスできるのでご相談ください。

↓今すぐフォローすべきキラキラアカウント

Follow @tdualdir

↓今すぐ登録すべきキラキラAIサービス
www.matrixflow.net

じゃあの。

2020-11-24

事業のわかるITエンジニアはどこにいるのか。

ワイ。

2020-07-13

形態素解析器比較 Sudachi vs Mecab+Neologd

Python gensim 機械学習自然言語処理 mecab sudachi

ブレインパッドさんのpodcast「白金鉱業.FM」の聞いてたらSudachiの開発の話を聞いて興味が出たので触ってみました。
shirokane-kougyou.fm
（「白金鉱業.FM」はデータ分析現場の生の声が聴けるのでなかなか面白いです。）

Sudachiとは
使ってみる
比較
結果
速度について
その他
- 品詞の付与について
終わりに

Sudachiとは

ワークスアプリケーションズ徳島人工知能 NLP研究所でオープンソース開発されている形態素解析器です。
www.worksap.co.jp

形態素解析器とは日本語を単語に分かち書きしたり、品詞を特定する機能を有するもので、日本語の自然言語処理では必須です。
同じ様なものにはMecabやJuman++などがあります。
Sudachiの強みは辞書にあるらしく、長年研究してる専門家が辞書のメンテナンスをしているそうです。
また、分かち書きの方法（モード）が複数あり、切る長さを選ぶことが出来ます。

使ってみる

pythonのモジュールはここにあります。
https://github.com/WorksApplications/SudachiPy

まずはインストールします。

pip install sudachipy # 本体のインストール
pip install sudachidict_core #辞書のインストール

インポートしてそれぞれモードで分かち書きしてみる。

from sudachipy import tokenizer
from sudachipy import dictionary

tokenizer_obj = dictionary.Dictionary().create()

モードA

mode = tokenizer.Tokenizer.SplitMode.A
[
    (
        m.surface(), 
        m.dictionary_form(), 
        m.reading_form(),
        m.part_of_speech()
    )
    for m in tokenizer_obj.tokenize("国家公務員", mode)]

出力:

[('国家', '国家', 'コッカ', ['名詞', '普通名詞', '一般', '*', '*', '*']),
 ('公務', '公務', 'コウム', ['名詞', '普通名詞', '一般', '*', '*', '*']),
 ('員', '員', 'イン', ['接尾辞', '名詞的', '一般', '*', '*', '*'])]

モードB

mode = tokenizer.Tokenizer.SplitMode.B
[
    (
        m.surface(), 
        m.dictionary_form(), 
        m.reading_form(),
        m.part_of_speech()
    )
    for m in tokenizer_obj.tokenize("国家公務員", mode)]

出力:

[('国家', '国家', 'コッカ', ['名詞', '普通名詞', '一般', '*', '*', '*']),
 ('公務員', '公務員', 'コウムイン', ['名詞', '普通名詞', '一般', '*', '*', '*'])]

モードC

mode = tokenizer.Tokenizer.SplitMode.C
[
    (
        m.surface(), 
        m.dictionary_form(), 
        m.reading_form(),
        m.part_of_speech()
    )
    for m in tokenizer_obj.tokenize("国家公務員", mode)]

出力:

[('国家公務員', '国家公務員', 'コッカコウムイン', ['名詞', '普通名詞', '一般', '*', '*', '*'])]

モードAは細かく分解するのに対してモードCはあまり分解しない様です。
モジュールとしての使い勝手としてもよさそうです。

また正規化もしてくれます。

tokenizer_obj.tokenize("SUMMER", mode)[0].normalized_form()

出力:

'サマー'

すばらしい。

比較

ニュース記事分類のタスクで性能を比較してみます。
具体的にはSudachiとMecab+Neologdで分かち書きしたものをそれぞれtf-idfでベクトル化してロジスティック回帰で分類してみます。

データセット

データセットにはお馴染み（？）のlivedoor ニュースコーパスを使います。
https://www.rondhuit.com/download.html#ldcc

9種類の記事があり全部で7376記事あります。

使用したモジュール

この辺のモジュールを使いました。

import re
import math
import resource
import numpy as np
from urllib import request 
from pathlib import Path


import MeCab
import neologdn
import gensim
from gensim import corpora
from gensim.corpora import Dictionary


import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.metrics import recall_score, precision_score, accuracy_score
from sklearn.linear_model import LogisticRegression

from sudachipy import tokenizer
from sudachipy import dictionary

トークナイザー

SudachiとMecabそれぞれに対してほぼ同じ処理をするトークナイザーを作りました。

class SudachiTokenizer():
    def __init__(self, mode="C", stopwords=None, include_pos=None):
        
        if mode not in ["A", "B", "C"]:
            raise Exception("invalid mode. 'A' ,'B' or 'C'")
        self.mode = getattr(tokenizer.Tokenizer.SplitMode, mode)
        print(self.mode )
        
        if stopwords is None:
            self.stopwords = []
        else:
            self.stopwords = stopwords
        if include_pos is None:
            self.include_pos = ["名詞", "動詞", "形容詞"]
        else:
            self.include_pos = include_pos
    
    def parser(self, text):
        return tokenizer_obj.tokenize(text, self.mode)
    
    
    def tokenize(self, text, pos=False):
        res = []
        for m in self.parser(text):
            p = m.part_of_speech()
            base = m.normalized_form() #.dictionary_form()
            #print(base, ": ", p)
            if p[0] in self.include_pos and base not in self.stopwords and p[1] != "数詞":
                if pos:
                    res.append((base, p[0]))
                else:
                    res.append(base)
        return res

class MeCabTokenizer:
    def __init__(self, dic_dir=None, stopwords=None, include_pos=None):
        tagger_cmd = "-Ochasen"
        if dic_dir:
            tagger_cmd += " -d {}".format(dic_dir)
        mecab = MeCab.Tagger(tagger_cmd)
        self.parser = mecab.parse
        if stopwords is None:
            self.stopwords = []
        else:
            self.stopwords = stopwords
        if include_pos is None:
            self.include_pos = ["名詞", "動詞", "形容詞"]
        else:
            self.include_pos = include_pos

    def tokenize(self, text, pos=False):
        l = [line.split("\t") for line in self.parser(text).split("\n")]
        res = []
        for w in l:
            if len(w) >=4: # check nomal words (e.g. not EOS)
                p = w[3]
                group_pos = p.split("-")[0]
                base = w[2]
                if group_pos in self.include_pos and base not in self.stopwords and "数" not in p:
                    if pos:
                        res.append((base, p))
                    else:
                        res.append(base)
        return res

また、これらのトークナイザーに通す前には共通の関数でノーマライズしてます。

kaomoji_reg = r'[\[|\(][^あ-ん\u30A1-\u30F4\u2E80-\u2FDF\u3005-\u3007\u3400-\u4DBF\u4E00-\u9FFF\uF900-\uFAFF\U00020000-\U0002EBEF]+?[\]|\)]'
m = re.compile(kaomoji_reg)
def normalize(text):
    text = str(text)
    text = text.replace("\n", " ")
    text = re.sub(r"http(s)?:\/{2}[\d\w-]+(\.[\d\w-]+)*(?:(?:\/[^\s/]*))*", "　", text)
    text = re.sub(r"\S*@\S*\s?" ,"　", text)
    text = text.lower()
    text = re.sub(kaomoji_reg, " ", text)
    text = re.sub(r'\d+', '', text)
    text = neologdn.normalize(text)
    return text

ストップワードも用意します。

sw_filename = "stopwords.txt"
if not Path(sw_filename).exists():
    res = request.urlopen("http://svn.sourceforge.jp/svnroot/slothlib/CSharp/Version1/SlothLib/NLP/Filter/StopWord/word/Japanese.txt").read().decode("utf-8")
    with open(sw_filename, "w") as f:
        f.write(res)
else:
    with open(sw_filename) as f:
        res = f.read()
stopwords = [line.strip() for line in res.split("\n")]
print(len(stopwords))　#331
print(stopwords[:3]) # ['あそこ', 'あたり', 'あちら']

トークナイザー使用例

include_pos = ["名詞", "動詞", "形容詞"]
mecab_tokenizer = MeCabTokenizer(dic_dir="/usr/local/lib/mecab/dic/mecab-ipadic-neologd", stopwords=stopwords, include_pos=include_pos)
sudachi_tokenizer = SudachiTokenizer(mode="B", stopwords=stopwords, include_pos=include_pos+["形状詞"])

mecab_tokenizer.tokenize(normalize(text), pos=False)
# 出力　['コード', '命令', '冗長', '算出', 'プロパティ', '利用', 'する', 'バージョン', '比較', 'する', 'みる']

sudachi_tokenizer.tokenize(normalize(text), pos=False)
# 出力　['コード', '命令', '冗長', '算出', 'プロパティー', '利用', '為る', 'バージョン', '比較', '為る', '見る']

「する」と「為る」、「みる」と「見る」の違いはsudachiのnormalized_form()から来ています。

辞書の統計的フィルター

今回は分類のタスクなので、全ての記事の中で1回しか出てない単語や、全体の9割より多く出現してる単語を除去しました。

dictinonary_mecab = Dictionary(sentences_mecab)
dictinonary_mecab.filter_extremes(no_below=2, no_above=0.9)
dictinonary_mecab.compactify()
corpus_mecab = [dictinonary_mecab.doc2bow(w) for w in sentences_mecab]

dictinonary_sudachi = Dictionary(sentences_sudachi)
dictinonary_sudachi.filter_extremes(no_below=2, no_above=0.9)
dictinonary_sudachi.compactify()
corpus_sudachi = [dictinonary_sudachi.doc2bow(w) for w in sentences_sudachi]

ベクトル化

tf-idfでベクトル化します。つまり一つの記事は語彙数次元のスパースなベクトルになります。
モジュールにはgensimを使いました。

分類器

分類器にはロジスティック回帰を使いました。
今回はweightの設定もハイパラのチューニングもせずにscikit-learnのデフォルト値で学習

結果

Sudachi(モードA)

f:id:tdualdir:20200713160434p:plain — sudachi_A

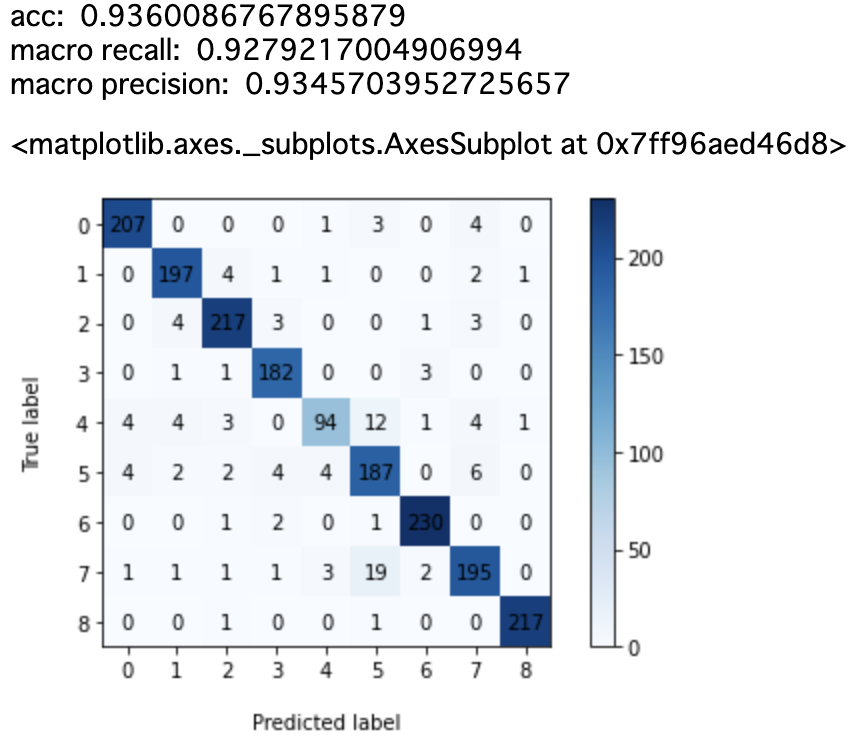
Sudachi(モードB)

f:id:tdualdir:20200713161020p:plain — sudachi_B

Sudachi(モードC)

f:id:tdualdir:20200713160721p:plain — sudachi_C

Mecab+Neologd

f:id:tdualdir:20200713154222p:plain — mecab

正解率
Sudachi(モードA) : 0.936
Sudachi(モードB) : 0.934
Sudachi(モードC) : 0.935
Mecab+Neologd: 0.943

Mecab+Neologdが一番良いです。

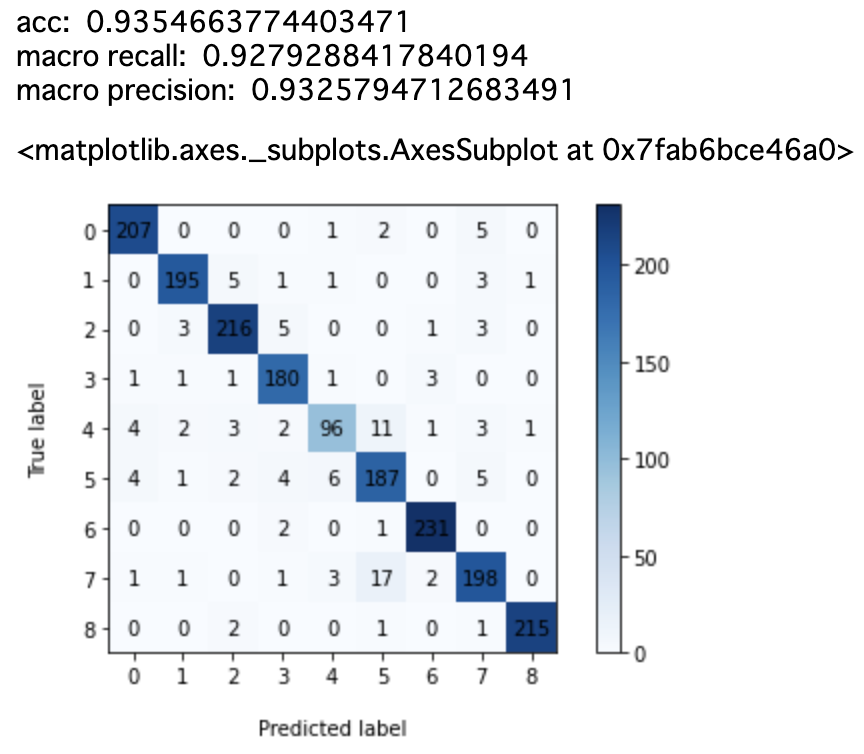
速度について

気になったのが速度です。
訓練データとして5532個のニュース記事をトークナイズした結果です。
f:id:tdualdir:20200713141431p:plain
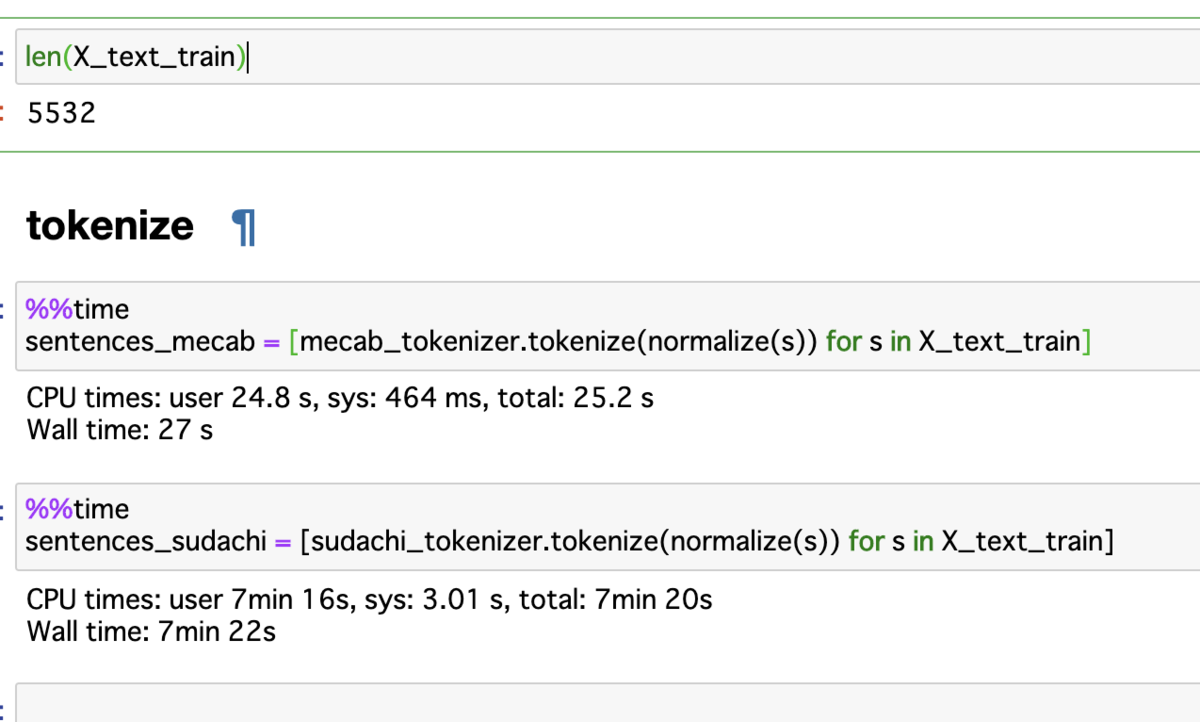
Mecabが30秒かからずに終わっていますが、Sudachiは７分３０秒ほどかかっています。

その他

品詞の付与について

品詞の特定はMecabとほとんど変わらないのですが、ちょいちょい違う場合もある様です。
f:id:tdualdir:20200713142212p:plain

なので今回は"名詞", "動詞", "形容詞"のみを抽出する予定でしたが、Sudachiの場合は"形状詞"も抽出しました。

終わりに

今回のタスクにおいてはMecab+Neologdの方が良かったです。
podcastでも少し言ってましたが、今は検索タスクを優先して改善してる様なので今回の使い方はまだフォーカスしてないのかもしれません。
この先10年はメンテしていく予定らしいので、ビジネスに使うとかシステムに組み込むという話になった時は一つ選択肢には上がると思います。
（組み込んだ後のNeologdの更新って皆んなどうしてるんだろう🤔）

また今回のコードはここにあります。こうした方が良いとかアドバイスください！
github.com

↓今すぐフォローすべきキラキラアカウント

Follow @tdualdir

↓今すぐ登録すべきキラキラAIサービス
www.matrixflow.net

じゃあの。

2020-07-03

くそだったワイが起業してやったこと。むしろやってない奴はやばい。

初めまして。株式会社MatrixFlow（マトリックスフロー）のCEOをやってるものです。
株式会社MatrixFlowは,ビジネスマン向けのAIを構築・活用・運用出来るプラットフォームサービス「MatrixFlow」を運営しています。
www.matrixflow.net
おかげさまでユーザーも2000名を超え、経済産業新聞さんや東洋経済さんに取り上げてもらってユーザーも週で20名以上伸びています。
会社自体はまだ2年も立ってないひよっこですが、経験を少しでもこれから起業しようと思ってる人、起業に興味がある人に還元できればと思ってます。

1.起業したら、アクセラレータープログラムに入る

スタートアップを各方面から支援するアクセラレータープログラムと言うものを大企業や行政が実施しています。
メンターの教えによる会社経営の示唆や知識は学びは大きく非常に感謝してます。
また、そこの業界ネットワークに参加できることも大きいです。今でもそこで築いたネットワーク関係で仕事が入って来てます。
同業種の同期であることの仲間意識は思った以上に強いです。
起業した際には是非とも自分の分野のアクセラレータープログラムを検索して申し込むことをオススメします。
（MatrixFlow社はバイトルでお馴染みのdipがやっているAIアクセラレーターと、海外VCのPlug and Playの日本法人がやってるアクセラレータプログラムに参加してます。）

2.VCからもらうのは資金よりも知恵や経験

起業したての頃にいくつかのVCをまわりました。
最初は資金調達を目的としてましたが、優秀なVCさんと話していると資金よりも知恵や数々のスタートアップを見て来た経験からくる助言が非常に重く役に立ちます。
もちろん腹が立つような言葉を浴びせられたこともありますが、今振り返ると決して間違ってることを言ってるわけではないのでVCの言うことはまずは素直に聞いて実践することをオススメします。
また、ラウンドが違うVCからは他のVCの紹介や仕事をもらったこともあるのでVCとは積極的に会うべきです。

3.ベンチャー融資の申請

日本金融公庫がスタートアップに対して最大2000万円の融資をしている。（2020年7月の現状）
受けない手はない。手続き等で不安がある場合は申請の手助けをするサービスもあるのでそこに頼るのもありです。

4.ツールに頼るべき

事業をやる上で専用のツールは沢山あるので有効活用すべき。間違ってもエクセルでなんとかしようと思うべきじゃない。
MatrixFlow社は
・進捗管理はTrello(無料）
・営業・カスタマーサクセスはHubspot（無料）
・会計はfreee(有料)
・コミュニケーションはslack(無料)
・Gsuite (メール、スライド、ドキュメント、スプレッドシート、アンケートフォーム等)　（有料）
を使っています。
少なくともslack、TrelloとHubspotは使うべき。

5.スタートアップ専門の弁護士をつける

弁護士っていうと大袈裟な感じがするが、スタートアップこそ不利な契約が結ばれそうになることがある（損害賠償の範囲も大きく賠償金の上限も無しなど）。
そこで創業2年以内なら格安のサービスをしてる事務所があるのでそこにお願いする。
MatrixFlow社はAZXにお願いしてる。（ちゃんと疑問にも答えてくれるので正直めっちゃ満足してる）

6.メディアには露出すべき

メディアにばっか出る経営者は胡散臭いとか自己顕示欲が強いとか言われがちだが、メディアの効果はやはり大きい。
MatrixFlow社もインタビュー記事きっかけで商談が組まれて最終的に数千万円の案件に繋がった。
よっぽど嫌ではなければメディアには露出した方が良い。

7.悪いのは常に自分

社員がミスをした時、悪いのは社員じゃなくてミスをするような体制を作ってる経営者である。
ミスは人ではなくてシステムが引き起こすと思ってシステムの改善をすべきです。
例えば、営業部の人が商談のあとのお礼メールを出すのを忘れるならカレンダーにお礼メールを出すというスケジュールを追加するようにしたり、管理ツールにお礼メールというチェックボックスを作ったりと人ベースではなくシステムベースでミスを減らす努力するのが経営者です。

8.取引相手が欲しいのは製品やサービスではなく、効果やメンツ

究極的なことを言えば、取引相手が欲しいのは質の高い製品・サービスではなくて、
そこから得られる効果やそれによって得られる組織内でのメンツであることを意識する。
如何に性能が良いかではくて、如何にこれの導入によって組織やあなたが得をするか言うべき。

おわり

まだありますが、長くなったのでこのあたりで一旦終了です！
好評ならpart2をやります。

↓今すぐフォローすべきキラキラアカウント

Follow @tdualdir

↓今すぐ登録すべきキラキラAIサービス
www.matrixflow.net

じゃあの。

2019-06-23

de:code2019に行ったらMicrosoftのAI戦略が見えてきた

お久しぶりです。半年ぶりくらいにブログを書きます。

5/29と5/30にザ・プリンスパークタワー東京で開催されたde:code2019に参加してきてました。
Microsoftが毎年開催しているエンジニア向けの一大イベントです。

www.microsoft.com

まずは「マイクロソフトリサーチの AI / 自然言語処理研究最前線」を聞きました。

#decode19 pic.twitter.com/ZezqiZAYrS
— tdual🔰MatrixFlow (@tdualdir) May 29, 2019

Microsoft Research のこれまでの自然言語処理の基礎研究の成果の紹介でした。
歴史の中でブレイクスルーに確実に絡んでいるのはさすがだなぁと思って聞いていました。
また「りんな」についても触れていて何かを効率化するAIではなく、Emotional AIだと言ってたのが印象に残りました。

次は「開発者のための機械学習入門：Azure Machine Learning Studio で構造化データから予測分析」を聞きました。

競合視察的なやつ #decode19 pic.twitter.com/NdaT9JZipk
— tdual🔰MatrixFlow (@tdualdir) May 29, 2019

目的は弊社が開発しているサービス「MatrixFlow」と似ているので敵状視察的なやつです。
セッションの内容としては機械学習の基本的な考え方から始まって後半からようやくML Studioの話が出てきました。
初めて知ったことも多かったです。
例えば、ML StudioはGUIで前処理や機械学習のトレーニングが可能で学習済みモデルをそのままWebサービスにデプロイできるのですが、モデルの更新はPower shellでやらないといけないと言う若干ズコー感がある事や、エクセルから推論テストが出来ることを知りました。
最後にはML Studioの上位互換になる（予定の？）Azure Machine Learning Service Visual Interface（まだプレビュー版）の説明もありました。
ML Studioと比べた時に何が変わったかと言うと、GPUが使用可能、デプロイ先がKubernatesを使えるようになったりとクラウドらしい構成になったようです。GA(General Available)が楽しみです。

個人的にはML Studioにエクセルのプラグインが用意され連携できるのがMicrosoftらしいと思いましたが、推論だけでもエクセル上からできると言うのはAIを意識的に使うのではなく、いつの間にか裏でAIが動いていたと言う世界を作るには良いのかもしれません🤔

１日目の最後は「Build 2019 Azure AI & Data Platform 最新アップデート」を聞きました。
機械学習系の話を期待して行ったのですが、ほとんどがDB周りの話でした。しかし面白かったです。
例のAzure SQL Database Serverless（まだプレビュー版）の話がありました。データベースの負荷が全くない場合はPausedして料金がゼロになると言うのはすごい。
またCosmos DBのSpark対応でSparkがCosmos DBと同じサーバー内にあるのでロードする必要なく使えると言うは面白いし実際に便利そうでした。

２日目の最初は「こうすれば Deep Learning 推論は速くなる！Intel AI ソフトウェア製品を活用した推論高速化手法のご紹介」を聞きました。
Intelのチップを効率よく使う方法やopenVINOの説明でした。
pip install intel-tensorflowでインテルチップ用にオプティマイズしたTensorflowが使えるなんて初めて知りました。
またopenVINOと言うインテルに特化した推論SDKも初耳でした。
物体検知のデモをやっていましたが、確かに早くなっていました。iGPUがあるならエッジでも爆速になるらしいです。

そしてなぜかこのツイートが若干伸びた

pip install intel-tensorflow
でインテルがオプティマイズしたtensorflowが使える　#decode19
— tdual🔰MatrixFlow (@tdualdir) May 30, 2019

次は「Custom Vision で出来ること & 出来ないからって諦めてませんか?」を聞きに行きました。
Custom Visionに特段興味があったわけではないですが、機械学習系のサービスとしてどう売り出しているのかを理解して最終的にMatrixFlowに活かそうと思って行きました。
どうやらディスカッション系のセッションだったらしくオーディエンスはスマホから質問を投稿し、それに答えていきつつオーディエンスにも積極的に質問をする形式でした。
登壇者も休むことなくずっと喋っていてエンターテイナーかwwwって思いました。
内容としては聞いているとCustom Visionは足がかりとしては良いかもしれないけど、色々制限があってガチで何かやろうとするにはまだ使いにくそうという印象でした。
ただ、dockerやiOS用にエクスポートできるのでエンジニアがPoCでサクッと何か作ってみるのには使えそうでした。

次は「機械学習のためのデータ加工～特徴量の見つけ方と作り方」を聞きました。

#decode19 pic.twitter.com/fiUfX2lexs
— tdual🔰MatrixFlow (@tdualdir) May 30, 2019

AutoMLが当たり前になっていく中で特徴量の作成は自動化出来ないので大事だと言う話をして、その後に失敗談を交えて特徴量の作り方の解説をしていました。
目的変数はビジネス課題になっているのかをしっかりと検討し、
説明変数は特徴量の洗い出しは5W2H (5W1H +how much)でやりモデルの活用のタイミングもイメージすべきという内容でした。
特徴量を作るときにビジネス課題を解決するためという視点を忘れてはいけないという非常に教育的なセッションでした。

最後に「Azure Machine Learning service Deep Dive ～自動機械学習から MLOps まで～」を聞きました。

#decode19 pic.twitter.com/JpSNkV9nTk
— tdual🔰MatrixFlow (@tdualdir) May 30, 2019

PoCを超え、機械学習をサービスとして提供してる会社が次に必要でなるであろうMLOps。それをAzure DevOpsの応用で実現するという内容でした。
自動化パイプラインで精度などのモニタリングまでやって再学習やデプロイのサイクルを効率的に回そうという話。
Azure Machine Learning Workspaceでモデルを一元管理できるんですね。良さそうです。
全体のパイプライン構成も精度などの監視も含めると割とアリな構成なんじゃないかと思いました。
また、最後の方でAutomated MLの紹介がありましたが、前処理も含めて自動化してくれるらしいです🤔
そしてそのAutomated MLはSHAP、LIMEをモロそのままサービスに組み込んでいるのもInterpretabilityの時流に乗っていて素晴らしいと感じました。

まとめ
仕事柄、競合調査の一環で機械学習系のツールやサービスの情報収集をすることが多いのですが、Microsoftの機械学習関係のサービスはチグハグ感があったのが今回のde:codeを通した印象としてはAzure上に綺麗にまとめて来ています。AIをAIとして世に提供するというよりはクラウドソリューションの一機能として提供したいという思いが伝わってきます。
エンタープライズに強いMicrosoftだからこそ、ビジネス活用されるAIのシェアはAzureと共に広げていくという戦略はシンプルで効果的だと思いました。

↓今すぐ登録すべきキラキラAIサービス
www.products.matrixflow.net

↓今すぐフォローすべきキラキラアカウント

Follow @tdualdir

じゃあの。

2018-11-09

私が実践した、エンジニアが超優良企業に転職するための最も簡単な方法

転職先を自分で作る。
（起業する。）

↓今すぐフォローすべきキラキラアカウント

Follow @tdualdir

↑今すぐフォローすべきキラキラアカウント

2018-05-19

PyCon mini OsakaでCharacter-Level CNNについて話してきた。

機械学習深層学習発表

スライド
Character-Level CNN
終わりに

東京在住ですが、なぜかグランフロント大阪で開催されたPyCon mini Osakaで登壇して来ました。
osaka.pycon.jp

前日から大阪に乗り込んでました。（久しぶりに弊社の大阪オフィスに行った。）

スライド

発表内容は以下のスライドになります。

Characeter-Level CNN from tdualdir

www.slideshare.net
（画像がぼやけていてすまない・・・）
最初はCNNやTensorFlowの基礎的な説明をして後半からCharacter-Level CNNについて話しました。

Character-Level CNN

Character-Level CNNのところを説明します。

Character-Level CNNとは

文書を文字（Character）単位で区切ってそれをCNNに通してテキスト分類します。　※単語単位でないのに注意

今回やること

今回は、テキストからネガティブかポジティブかを判断するタスク（いわゆる感情分析のネガポジ）をこなす分類器を作ることを考えます。
結果から言うと、オリジナル論文*1では上手く行かずに、違うアーキテクチャで上手く行きました。

なぜ文字レベルなのか？

文字レベルで自然言語処理をするというのは珍しいと思いますが（大体は単語レベルで区切る）、そのメリットは

前処理がいらない（日本語なら分かち書きが必要ない）
タイポやスペルミスが多い文書でも有効（レビュー,チャットなど）
文書じゃない物にも適応できる（URL, Tex, プログラミングコードなど）

などが挙げられます。

論文

上手くいったアーキテクチャですが、
Joshua Saxe, Konstantin Berlin: eXpose:A Character-Level Convolutional Neural Network with Embeddings For Detecting Malicious URLs, File Paths and Registry Keys(https://arxiv.org/abs/1702.08568)
を参考にしました。
内容はCharacter-Level CNNを使って悪意あるURLやファイルパスを検出するという内容です。
かなり丁寧に書かれていてわかりやすい論文でした。

構成・アーキテクチャ

処理の流れとしては

文字を低次元に埋め込む
カーネルサイズが違う複数のCNNに入れて特徴を出力
特徴を一つに結合
全結合層に通して分類

です。

1の埋め込みは、（文字 × 埋め込み次元）行列を埋め込み層として用意して、対応する文字の行ベクトルだけを更新します。

f:id:tdualdir:20180520142008p:plain:w300 — 図1.埋め込み層

2については論文に書いてる図を借りると次のようになります。

f:id:tdualdir:20180519210753p:plain — 図２.CNNの処理

1×2,1×3,1×4,1×5というサイズのフィルターにそれぞれ通します。
様々なWindowで文字のCooccurrence(共起性)を学習してると考えられます。

f:id:tdualdir:20180519211149p:plain — 図3.CNN部分の解釈

3.特徴を一つに結合、4.全結合層に通して分類はそのままの意味です。

TensorFlowで実装してTensorboardのグラフに書くと以下のようになります。

f:id:tdualdir:20180519205644p:plain — 図4.アーキテクチャ

日本語のデータセット

日本語のデータセットとして最近公表されたばかりのchABSA-dataset*2を使いました。
上場企業の有価証券報告書をベースに作成されたデータセットで、特徴としては「何が」ポジティブ/ネガティブだったのかと言う情報を含んでいます。
これで、「何が」のネガティブとポジティブの数を比べて多い方を文書全体の感情としました。
その結果、訓練データとテストデータを合わせて2830文書が対象となりました。