LDAとそれでニュース記事レコメンドを作った。

筆不精なのでこのブログも放置気味だったのですが、まあ流石にそろそろ少しずつでも今まで貯めた込んだものを書き残した方が良い気がしてきた。
なので、これからなんか書いていきます。

最初はDeep Learningの記事にしようとも思ったけど、社内勉強会でLDAをまとめてたのを思い出したのでまずはこれから書こうと思います。

注意書き
理論
実践
終わりに

注意書き

・理論編と実践編の二部構成になっています。

・理論編で扱うLDAの学習アルゴリズムですが、崩壊型ギブスサンプリングの解説や実装はWEB上にいくらでも見つかるのでこの記事では変分ベイズの解説をします。

・実践編で使うプログラミング言語はPython３です。

・記事レコメンドの作成には主にgensimを使ってます。

・記事レコメンドのデータセットとして、livedoor ニュースコーパスを使っています。

・この記事の内容は業務とは無関係です。私の趣味の内容です。

理論

1.LDAの前に「トピックモデル」とは

LDAはトピックモデルの手法の一つです。なのでまずはトピックモデルについて理解する必要があります。

トピックモデルとはデータが「潜在的な意味のカテゴリ」から生成されると仮定したモデルです。
この「潜在的な意味のカテゴリ」の事をトピックと呼びます。
（自然言語処理ではこのデータは主に文書の集合なので以降は文書を例に説明していきたいと思います。）

このトピックとは何なのか分かりにくいので具体例を考えましょう。
図１の様な二つの単語の分布があったとしましょう。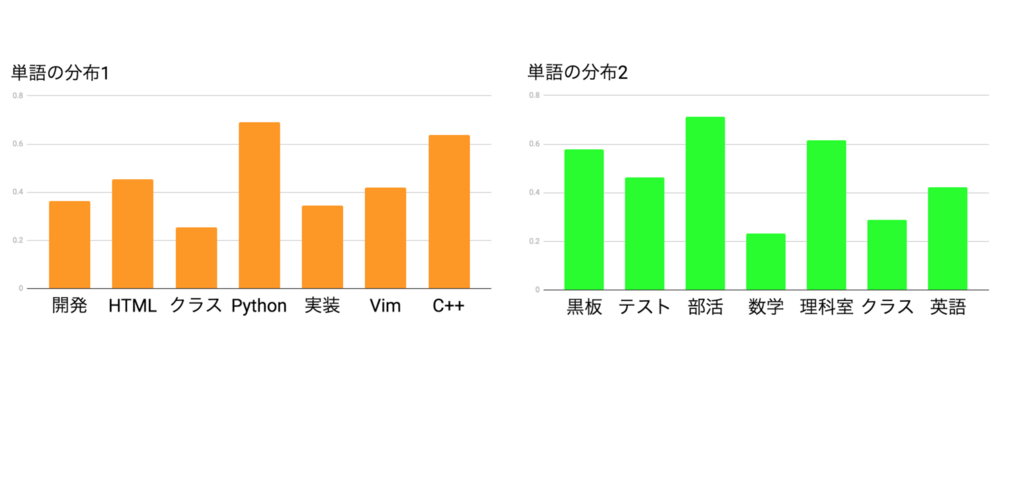

f:id:tdualdir:20180406101353p:plain — 図1.単語分布例

左側の「単語の分布１」を見た時に出て来ている単語に共通の意味がありそうな気がします。
「プログラミング」に関係してそうな単語が揃っていますね。
一方で右側の「単語の分布2」は「学校」に関係する単語だと気付くと思います。
つまり、これらの単語の分布には何らかの意味的なカテゴリがあり、この単語の分布がトピックなのです。

そして重要なのは「単語の分布１」にも「単語の分布２」にも「クラス」という同じ単語がありますが、意味が全く違う物を想像したはずです。
なぜ同じ「クラス」という単語を違うものとして想像したのでしょうか？
「開発」、「HTML」、「Python」などと一緒に「クラス」という単語があるときにこの「クラス」はきっと周りの単語と似た意味を持ってるはずだと思ったからです。周りの単語と見比べてそこで意味を推し量った結果、学級の「クラス」ではなくプログラミング言語のオブジェクト指向の「クラス」だと判断したのではないでしょうか。
つまり、単語には一対一に対応する意味があるのではなく、単語の共起性（co-occurrence）によって意味が作られると考えられます。

これは文書中に現れる単語に関しても同じことが言えそうです。
文書中で急に全くが異なる意味の単語が出てくるとは考えにくいです。
なので、文書を単語の多重集合（Bag of Words（BOW））*1で表現し、単語の共起性がトピックを形成し、それを元に文書が生成されていると考えると文書の意味解析ができそうです。
これがトピックモデルの考え方です。

2.LDAとは*2

・Latent Dirichlet Allocationの略。日本語では「潜在ディリクレ分配法」
・トピックモデルの手法の一つ
・確率的生成モデル
・ベイズ推定を使う
・文書はトピックの分布から（複数のトピックから）生成され、トピック分布はDirichlet分布に従う。

これだけ見ても何もわからないので説明していきます。

3.LDAで使う確率分布

まずLDAで使う確率分布を紹介します。

カテゴリカル分布（マルチヌーイ分布）

離散値 $\left(1,2,...,k\right)={\bf x}$ から1つ選ぶ時にそれぞれの値が選ばれる確率を $(p_1,p_2,...,p_k)={\bf p}$ とした時に次のような分布になります。（例えば目の出る確率が均等に出ないサイコロを振った時の確率）

$Cat_{k}\left({\bf x} \mid{\bf p} \right)=\prod_{i=1}^kp_i^{x_i} \tag{1}$
但し、 $x_i$ は0か1の値で、k個要素の中で1となるのは唯一つだけです。また、 ${\bf p}$ は確率なので $p_i \geq 0, \sum_{i=1}^k p_i=1$ を満たします。

特に ${\bf x}$ の中からnが選ばれると言うときは次の表記が出来ますね。
$Cat_k\left(x=n \mid{\bf p} \right)=\prod_{i=1}^kp_i^{\delta_{n,i}} \tag{2}$

$\delta_{n,i}$ はKronecker(クロネッカー)のデルタ*3です。

ちなみにBernoulli（ベルヌーイ）分布の複数事象バージョンなのでMultinoulli(マルチヌーイ)分布と呼ばれることもあります。

Dirichlet(ディリクレ)分布

k個の独立な事象の中でi番目の事象が $\alpha_{i}-1$ 回起きた場合にその事象の確率が $\theta_i$ になる確率分布をDirichlet分布と言います。

${\displaystyle Dir_k\left(\theta \mid \alpha \right)=\frac{\Gamma \left(\sum_{i=1}^k \alpha_i \right)}{ \prod^k_{i=1}\Gamma(\alpha_i)}\prod_{i=1}^k \theta_{i}^{\alpha_i - 1} \tag{3} }$

$\theta$ は確率なので、 $\theta_i \geq 0, \sum_{i=1}^k \theta_i=1$ を満たします。

係数にガンマ関数など色々付いてますが、全事象の確率を１にするための規格化係数なのであまり気にしなくても良いです。

4.確率的生成モデル

トピックがどのような単語の分布なのか、文書とトピック分布の形などは未知であり、我々が知っているのは文書に出てくる単語だけです。なので、未知変数を確率変数とし文書を生成する過程を記述する事で未知変数を推定します。これを確率的生成モデルと言います。

LDAでは全ての文書の生成確率を次のようにします。
$p(D\mid\alpha,\eta)=\prod_{d=1}^M \int Dir_k( \theta_d\mid\alpha)\prod^{N_d}_{n=1}\sum_{z_{dn}}^k\int p\left(z_{dn}\mid\theta_d \right)p\left(w_{dn}\mid z_{dn},\beta_{z_{dn}}\right)p(\beta_{z_{dn}}\mid\eta)d\beta_{z_{dn}}d\theta_d\tag{4}$

$M$ ：文書の数
$N_d$ : d番目文書に含まれる単語の数
$k$ ：トピックの数
$D$ ：全ての文書, $D = \left({\bf w}_1, {\bf w}_2, ...,{\bf w}_d, {\bf w}_{d+1},... {\bf w}_M\right)$
${\bf w}_d$ : d番目の文書, ${\bf w}_d = \left(w_{d1}, w_{d2}, ..., w_{dn},w_{d(n+1)},...,w_{dN_{d}} \right)$
$w_{dn}$ : d番目文書のn番目単語
$z_{dn}$ : d番目文書のn番目単語のトピック, $z_{dn} \in \{1,2,...,i,i+1,...,k \}$
$V$ : 語彙数（全文書に現れる単語の種類）

$Dir_k\left( \theta_d \mid \alpha \right)$ : d番目文書のトピック分布の生成

$p\left(z_{dn} \mid \theta_d \right)$ ：トピック $z_{dn}$ の生成分布
　　ここではこの分布はカテゴリカル分布とする。
　　 $p\left(z_{dn} \mid \theta_d \right)=Cat_k\left(z_{dn} \mid \theta_d \right)$

$p\left(w_{dn} \mid z_{dn},\beta_{z_{dn}} \right)$ ：単語 $w_{dn}$ の生成分布
　　ここではこの分布はカテゴリカル分布とする。
　　 $p\left(w_{dn} \mid z_{dn},\beta_{z_{dn}} \right)=Cat_V\left(w_{dn} \mid \beta_{z_{dn}} \right)$

$p\left(\beta_{z_{dn}} \mid \eta \right)$ ：トピック $z_{dn}$ の単語分布の生成
　　ここではこの分布もDirichlet分布とする。
　　 $p\left(\beta_{z_{dn}} \mid \eta \right) = Dir_V\left(\beta_{z_{dn}} \mid \eta \right)$

$\alpha, \eta$ がパラメータで実世界の文書を上手く表現するためにはこのパラメータの適切な値が分かれば良いという事になります。

5.グラフィカルモデル表現

式(4)では分かりにくいので直感的に理解する為の道具としてグラフィカルモデル表現があります。（LDAではこのグラフィカルモデルの方が有名かも？）

f:id:tdualdir:20180214101658p:plain — 図2.グラフィカルモデル表現

円（ノード）がそれぞれ確率分布を表してます。
黒色に塗りつぶされた円が観測変数の確率分布、白色の円が未知変数の確率分布を表してます。
また矢印元の円が矢印先の条件を表してます。
k,N,Mと名前がついたプレートは変数の数を表してます。これで変数の数だけ矢印を伸ばすのを一回で表現しています。

（グラフィカルモデル表現のより詳しい解説はPRMLにあるのでそれを参照してください。）

6.LDAの解釈

何をしているかまだ分かりにくいので幾何的な解釈をしてみます。

簡単のためにこの世に「本」「空気」「読む」という単語しか存在しないとする。
全ての文書はこの3つの単語の分布から構成されている。
それぞれの生成確率の和は１になるので、文書は(3-1)次元単体（simplex）*4が上に存在することになる。

f:id:tdualdir:20180326162844p:plain:w200 — 図3.単語simplex

自然な文書の分布を取った場合にこの面上に一様に分布するでしょうか？
そんなことは無さそうだと分かります。なぜなら「"本"を"読む"」「"空気"を"読む"」は頻出しそうですが、"本"と"空気"は同じ文書に現れることは稀です。
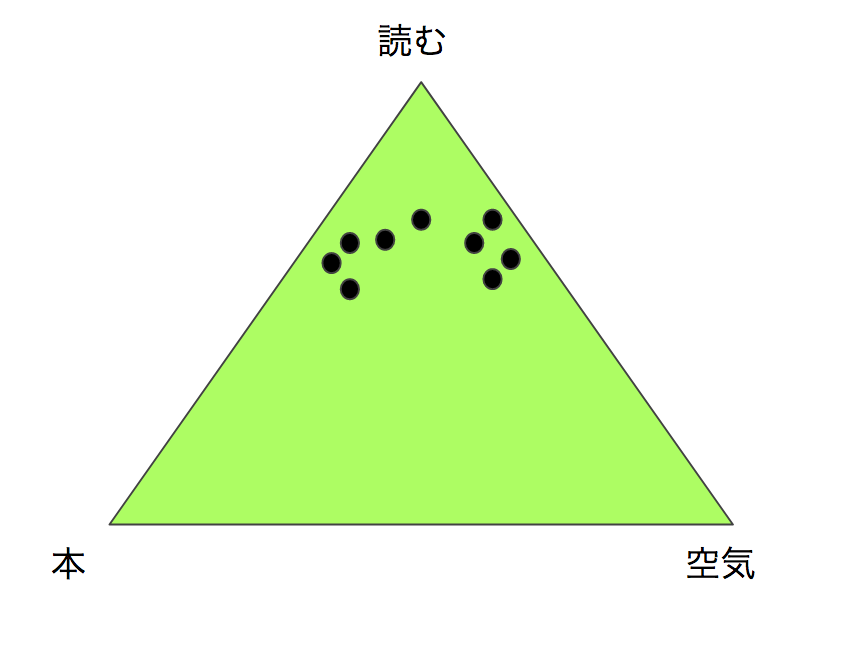
simpex上で言うならそれぞれの単語軸の値を(本,空気,読む)とするなら、(1/3,1/3,1/3)や(1/2,1/2,0)よりも (1/3,0,2/3)や(0,2/3,1/3)のような値付近に文書は分布するでしょう。

おそらく図4(a)のような分布になります。
この様な分布の偏りがあるなら低次元で表現できそうです。

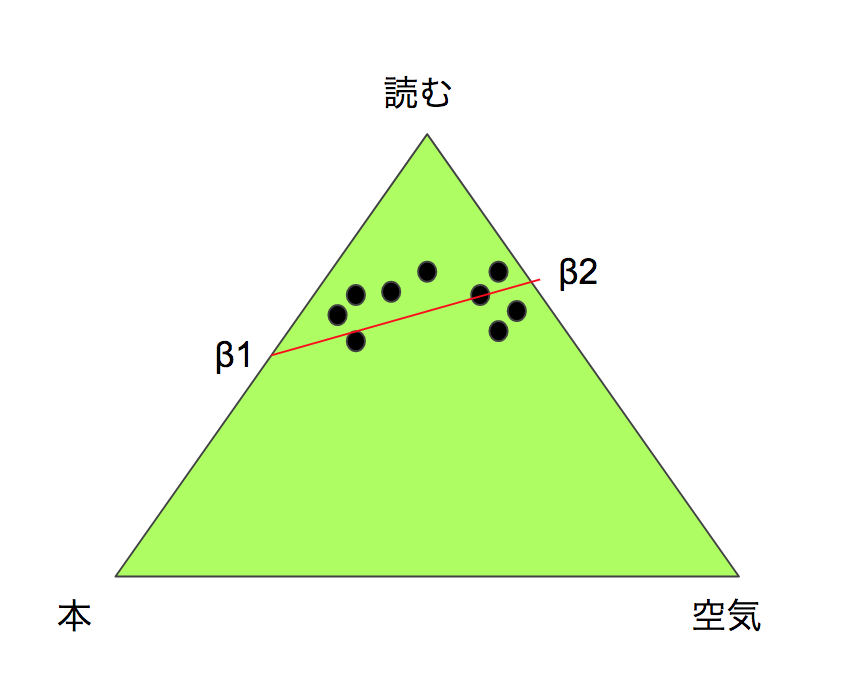
図4(b)の様に単語simplexより低次元のsimplex（赤い線分）で表現できるでしょう。その元をβ1、β2とします。

このβ1,β2がトピックであり、文書はこの赤い線分上に射影します。LDAはこれを(V-1)次元simplexでやっているのです。

文書が潜在的（Latent）な意味（トピック）で作られるsimplex上に配置（Allocation）されています。これがLDAの名前の由来です。

f:id:tdualdir:20180326163112p:plain — 図4(a). 単語simplex上の文書の分布　　　図4(b).低次元simplexへの写像

f:id:tdualdir:20180326162852p:plain — 図4(a). 単語simplex上の文書の分布　　　図4(b).低次元simplexへの写像

同じことですが行列分解的な解釈もできます。

式(4)の中には $\theta, \beta$ を与えた時にd番目文書のn番目単語の生成確率があります。

$\sum_{z_{dn}}^k p(z_{dn} \mid \theta_d) p(w_{dn} \mid z_{dn},\beta_{z_{dn}})$

d番目文書のn番目単語をwとし、わかりやすくするために $z_{dn}=i$ とラベルし直す。二つの確率分布がカテゴリカル分布なので、
$\sum_{z_{dn}}^k p(z_{dn} \mid \theta_d) p(w_{dn} \mid z_{dn},\beta_{z_{dn}}) = \sum_{i}^k \theta_{di}\beta_{iw}=\Theta B$
となります。

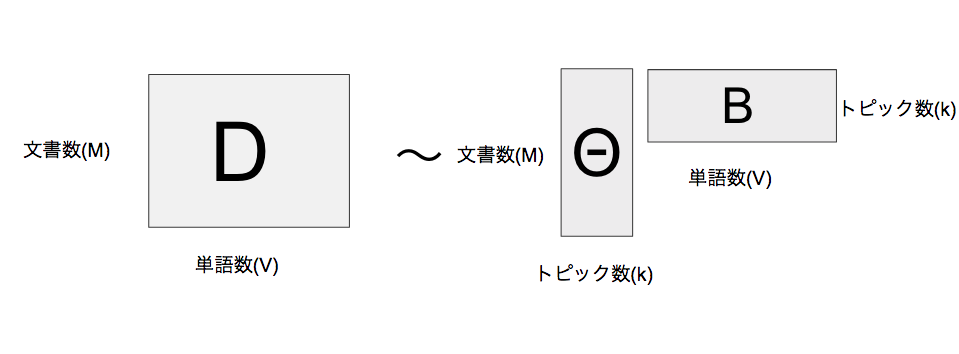
これは図5の様に（M,V）行列が低ランクの（M,i）行列と（i,V）行列に分解していると解釈できます。

f:id:tdualdir:20180223162022p:plain — 図5.行列分解

7.経験ベイズ(Empirical Bayes)

$\alpha, \eta$ を推定したいわけですが、経験ベイズで推定したと思います。

経験ベイズとは、データから事前分布を与える方法です。通常、事前分布はデータと関係なく与えるものですが経験ベイズではデータから事前分布のパラメータを推定します。（だから経験的と呼ばれてます。たぶん。）
パラメータを周辺化してしまってその尤度（周辺尤度という）を最大化します。
周辺尤度は式(4)と同じですが、こんな積分は計算できないので簡単な分布に近似して計算することを考えます。有名な方法にサンプリング法*5と「変分ベイズ法」がありますが、今回は変分ベイズ法を用います。

8.変分ベイズ法(Variational Bayesian methods)

まず後の議論を分かりやすくするために被積分関数を簡略化して表現します。
また次の様な表記を導入します。

$\theta=\left( \theta_1, \theta_2,..., \theta_M\right)$
$\beta=\left(\beta_1,\beta_2,...,\beta_k\right)$
$z=\left(z_{11},z_{12},...,z_{1N_{1}},z_{21},.....,z_{MN_{M}} \right)$
$p\left(D, z, \theta, \beta | \alpha,\eta \right) = Dir_k( \theta \mid \alpha) p\left(z \mid \theta \right) p\left(D\mid z,\eta \right) Dir_v\left(\beta \mid \eta \right)$

そして、いつものようにlogを取ります。*6
$\log p\left(D \mid \alpha,\eta \right) = \log \sum_z \int \int p\left(D, z, \theta, \beta | \alpha,\eta \right) d\beta d\theta \tag{5}$

先にも話したようにこのままでは計算できないので、 $p\left(D,z, \theta, \beta | \alpha,\eta \right)$ に近いなん
からかの分布を用意します。そのなんらかの分布を $q(z, \theta,\beta)$ として周辺尤度に差し込みます。
$\log p(D \mid \alpha,\eta) = \log \sum_z \int \int q(z, \theta,\beta)\frac{p(D, z, \theta, \beta \mid \alpha,\eta)}{q(z, \theta,\beta)} d\beta d\theta \tag{6}$
ここでJensenの不等式*7を使うと下限が存在することがわかります。

$\log \left(\sum_z \int \int q(z, \theta,\beta)\frac{p(D,z, \theta, \beta \mid \alpha,\eta)}{q(z, \theta,\beta)}d\beta d\theta \right) \geq \sum_z \int \int q(z, \theta,\beta) \log \frac{p\left(D, z, \theta, \beta \mid \alpha,\eta \right)}{q(z, \theta,\beta)}d\beta d\theta \tag{7}$
この下限を変分下限(Variational Lower Bound)やELBO(Evidence Lower Bound)と言います。（以降この変分下限を $\mathcal L$ と表記します。）

周辺尤度を大きくしたければ変分下限を最大化すれば良いことが分かります。

9.平均場近似(Mean field approximation)

しかしまだ計算が面倒臭いので思い切って、qをそれぞれのパラメータで独立な確率分布とします。これを平均場近似と言います。

$q(z, \theta,\beta) = q(z)q( \theta)q(\beta) \tag{8}$

但し、確率分布なので全て足し合わせると１になります。
${\displaystyle \sum_z q(z) = 1, \int q(\theta)d\theta=1, \int q(\beta)d\beta=1 \tag{9} }$
これを変分下限 $\mathcal L$ に代入して最大となる $q(z)q(\theta)q(\beta)$ を求めます。

10.変分下限とKullback-Leibler divergenceとの関係

Kullback–Leibler divergence(カルバック・ライブラー・ダイバージェンス以降、KL divergenceと呼ぶ)*8との関係を見るために変分下限を少し式変形します。

$\begin{align} \mathcal L &= \sum_z \int \int q(z, \theta,\beta) \log\frac{p\left(D,z, \theta,\beta\mid\alpha,η \right)}{q(z, \theta,\beta)} d\beta d \theta \\\ &=\sum_z \int \int q(z, \theta,\beta) \log \frac{p\left(z, \theta,\beta\mid D, \alpha,η \right)p\left(D\mid \alpha,η \right)}{q(z, \theta,\beta)} d\beta d \theta\\\ &= \sum_z \int \int q(z, \theta,\beta) \log \frac{p\left(z, \theta,\beta|D,\alpha,η \right)}{q(z, \theta,\beta)} d\beta d \theta + \sum_z \int \int q(z, \theta,\beta) \log p\left(D\mid \alpha,η \right)d\theta d\beta\\\ &= - D_{KL}(q(z, \theta,\beta) \mid p\left(z, \theta,\beta\mid D, \alpha,η \right)) + \log p\left(D\mid \alpha,η \right) \sum_z q(z) \int q(\beta) d\beta\int q( \theta)d \theta \\\ &= - D_{KL}(q(z, \theta,\beta) |p\left(z, \theta,\beta\mid D, \alpha,η \right)) + \log p\left(D\mid\alpha,η \right) \end{align}$

１項目にKL divergence、2項目に周辺尤度が出てくることに気付きます。

周辺尤度は $q(z)q( \theta)q(\beta)$ に依存してないので、変分下限を大きくすることはKL divergenceをなるべく小さくすることに相当します。つまり、用意したなんかよくわからん分布 $q\left(z, \theta,\beta \right)$ を $p\left(D,z, \theta, \beta \mid \alpha,\eta \right)$ に近づけることに他なりません。

11.変分法(Calculus of variations)

式からわかるように $\mathcal L$ は $q(z), q( \theta), q(\beta)$ に依存するので次のように書くべきです。
${\displaystyle \mathcal L=\mathcal L\left(q(z),q( \theta),q(\beta) \right) \tag{10} }$
この $\mathcal L\left(q(z),q( \theta),q(\beta) \right)$ の様な「関数の関数」のことを汎関数 *9といい、汎関数の極値になる時の関数を求める方法を変分法と言います。具体的に変分法を計算するにはEuler-Lagrange方程式*10という微分方程式を使います。ここで、
${\displaystyle \mathcal L\left(q(z),q( \theta),q(\beta) \right)=\sum_z\int\int L\left(q(z),q( \theta),q(\beta) \right)d\beta d\theta \tag{11} }$
${\displaystyle L\left(q(z),q( \theta),q(\beta) \right) = q(z)q( \theta)q(\beta) \log \frac{p\left(D,z, \theta, \beta \mid \alpha,\eta \right)}{q(z)q( \theta)q(\beta)} \tag{12} }$

とします。また、確率分布には(9)という拘束条件があるのでLagrangeの未定乗数法*11よりLは
${\displaystyle L' = L +\lambda_1\left(\sum_z q(z) - 1 \right) + \lambda_2\left(\int q( \theta)d\theta-1 \right) +\lambda_3\left(\int q(\beta)d\beta-1 \right) \tag{13} }$
となります。それぞれの確率分布に付いてEuler-Lagrange方程式を書くと

$q(\theta)$ については
${\displaystyle \sum_z \int \frac{\partial L'}{\partial q( \theta)} d\beta = 0 \tag{14} }$

$q(\beta)$ については
${\displaystyle \sum_z \int \frac{\partial L'}{\partial q(\beta)}d \theta = 0 \tag{15} }$

$q(z)$ については
${\displaystyle \int \int \frac{\partial L'}{\partial q(z)} d\beta d\theta = 0 \tag{16} }$

となる。（いずれも関数のパラメータの微分が無いので簡単な式になる。）

(14)をさらに計算する。

${\displaystyle \sum_z \int q(z)q(\beta)\log p(D, z, \theta, \beta \mid \alpha, \eta) d\beta - \log q(\theta) \sum_z q(z)\int q(\beta) d\beta + C +\lambda_2= 0 }$

Cは定数

（例えば、 $\int q(\beta)\log q(\beta) d\beta$ みたいな式などが出てくるけど $\theta$ にとっては所詮定数なので全てCにまとめました。 $\lambda_2$ もCに入れてしまって、以降すべての定数は値が違ってもCと表記します。）

$q(\theta)$ について解くと
${\displaystyle q(\theta) = C\exp\left(\sum_z \int q(z)q(\beta)\log p(D, z, \theta, \beta \mid \alpha, \eta) d\beta \right) \tag{14'} }$

同様に、 $q(\beta)$ について解くと
${\displaystyle q(\beta) = C\exp\left(\sum_z \int q(z)q(\theta)\log p(D, z, \theta, \beta \mid \alpha, \eta) d\theta \right) \tag{15'} }$

$q(z)$ についても解くと
${\displaystyle q(z) = C\exp\left(\int \int q(\theta)q(\beta)\log p(D, z, \theta, \beta \mid \alpha, \eta) d\beta d\theta \right) \tag{16'} }$

また、
${\displaystyle p\left(D, z, \theta, \beta \mid \alpha,\eta \right) =Dir_k( \theta \mid \alpha) p\left(z \mid \theta \right) p\left(D \mid z,\eta \right) Dir_v\left(\beta \mid \eta \right) }$
だったので(14')をさらに計算すると以下のようになります。

\begin{align}
q(\theta) &= C\exp\left(\sum_z \int q(z)q(\beta)\log Dir_k( \theta \mid \alpha) d\beta +\sum_z \int q(z)q(\beta)\log p\left(z \mid \theta \right)d\beta \right)\\
&= C\exp\left(\log Dir_k( \theta \mid \alpha) + E_{q(z)}\left[\log p\left(z \mid \theta \right) \right] \right)\\
&=C\exp\left(\sum_{d=1}^M\log \frac{\Gamma \left(\sum_i^k \alpha_i \right)}{\prod^k_i\Gamma(\alpha_i)}\prod_i^k \theta_{di}^{\alpha_i - 1} + E_{q(z)}\left[\log \prod_{d=1}^M\prod_{n=1}^{N_d}p\left(z_{dn} \mid \theta_d \right) \right] \right)\\
&=C\exp\left(\sum_{d=1}^M\log \prod_i^k \theta_{di}^{\alpha_i - 1} + E_{q(z)}\left[\log \prod_{d=1}^M\prod_{n=1}^{N_d}\prod_{i=1}^k \theta_{di}^{\delta_{z_{dn},i}} \right] \right)\\
&=C\exp\left(\sum_{d=1}^M\sum_{i=1}^k\log \theta_{di}^{\alpha_i - 1} + \sum_z\left[q(z)\sum_{d=1}^M\sum_{n=1}^{N_d}\sum_{i=1}^k\delta_{z_{dn},i}\log \theta_{di} \right] \right)\\
&=C\exp\left(\sum_{d=1}^M\sum_{i=1}^k\log \theta_{di}^{\alpha_i - 1} + \sum_{d=1}^M\sum_{i=1}^k\sum_{n=1}^{N_d}q(z_{dn}=i)\log \theta_{di} \right)\\
&=C\exp\left(\sum_{d=1}^M\sum_{i=1}^k\log \theta_{di}^{\alpha_i - 1} + \sum_{d=1}^M\sum_{i=1}^k\log \theta_{di}^{\sum_{n=1}^{N_d}q(z_{dn}=i)} \right)\\
&=C\prod_{d=1}^M\prod_{i=1}^k \theta_{di}^{\alpha_i+\sum_{n=1}^{N_d}q(z_{dn}=i)-1}\\
&=\prod_{d=1}^M Dir_k( \theta_d\mid\gamma_d)
\end{align}

但し、 $\gamma_d=(\gamma_{d1},\gamma_{d2},...,\gamma_{dk})$ ,
${\displaystyle \gamma_{di}=\alpha_i+\sum_{n=1}^{N_d}q(z_{dn}=i) \tag{17} }$
3行目から4行目への変換はDirichlet分布の係数をCに入れてしまいました。また、

$p\left(z_{dn} \mid \theta_d \right)$ がカテゴリカル分布なので、 $p\left(z_{dn} \mid \theta_d \right) =prod_{i=1}^k p\left(z_{dn}=i \mid \theta_d \right)=\prod_{i=1}^k \theta_{di}^{\delta_{z_{dn},i}}$ となる。

また、最後の式は規格化するようにCを選びました。

$q(\theta)$ はDirichlet分布になりました。

$q(\beta)$ の(13')に付いても計算すると、

\begin{align}
q(\beta) &= C\exp\left( \sum_z \int q(x) q(\theta) \log p(D\mid z,\beta)d\theta + \log Dir_v(\beta \mid η) \right)\\
&=C\exp\left(E_{q(z)}\left[\log p(D\mid z,\beta) \right]+\log \prod_{i=1}^k Dir_v(\beta_i\mid η) \right)\\
&=C\exp\left(E_{q(z)}\left[\log \prod_{d=1}^M\prod_{n=1}^{N_{d}} p(w_{dn} \mid z_{dn},\beta_{z_{dn}})\right]+\sum_{i=1}^k\log \frac{\Gamma \left(\sum_{w}^{V}η_{w} \right)}{\prod^{V}_{w}\Gamma(η_{w})}\prod_{w=1}^{V}\beta_{iw}^{η_{w} - 1} \right)\\
&=C\exp\left(E_{q(z)}\left[\log \prod_{d=1}^M\prod_{n=1}^{N_{d}}\prod_{i=1}^k\beta_{iw_{dn}}^{\delta_{z_{dn},i}} \right]+\sum_{i=1}^k\sum_{w=1}^V\log\beta_{iw}^{η_w - 1} \right)\\
&=C\exp\left(\sum_zq(z)\sum_{d=1}^M\sum_{n=1}^{N_{d}}\sum_{i=1}^k\delta_{z_{dn},i}\log\beta_{iw_{dn}}+\sum_{i=1}^k\sum_{w=1}^V\log\beta_{iw}^{η_w - 1} \right)\\
&=C\exp\left(\sum_{d=1}^M\sum_{n=1}^{N_{d}}\sum_{i=1}^kq(z_{dn}=i)\log\beta_{iw_{dn}}+\sum_{i=1}^k\sum_{w=1}^V\log\beta_{iw}^{η_w - 1} \right)\\
&=C\exp\left(\sum_{d=1}^M\sum_{n=1}^{N_{d}}\sum_{i=1}^k\sum_{w=1}^V\delta_{w, w_{dn}}q(z_{dn}=i)\log\beta_{iw}+\sum_{i=1}^k\sum_{w=1}^V\log\beta_{iw}^{η_w - 1} \right)\\
&=C\exp\left(\sum_{i=1}^k\sum_{w=1}^V\log\beta_{iw}^{\sum_{d=1}^M\sum_{n=1}^{N_{d}}\delta_{w, w_{dn}}q(z_{dn}=i)}+\sum_{i=1}^k\sum_{w=1}^V\log\beta_{iw}^{η_w - 1} \right)\\
&=C\prod_{i=1}^k\prod_{w=1}^V\beta_{iw}^{η_w+\sum_{d=1}^M\sum_{n=1}^{N_{d}}\delta_{w, w_{dn}}q(z_{dn}=i)-1}\\
&=\prod_{i=1}^kDir_{V}\left(\beta_i\mid\lambda \right)
\end{align}

但し、 $\lambda=(\lambda_1,\lambda_2,...,\lambda_V)$ ,
${\displaystyle \lambda_w=η_w+\sum_{d=1}^M\sum_{n=1}^{N_{d}}\delta_{w, w_{dn}}q(z_{dn}=i) \tag{18} }$
$q(\beta)$ もDirechlet分布になりました。

$q(z)$ の(16')についても計算すると、

\begin{align}
q(z) &= C\exp\left(\int \int q(\theta)q(\beta)\log p(D, z, \theta,\beta\mid\alpha,η)d\beta d\theta \right)\\
&=C\exp\left(\int \int q( \theta)q(\beta)(\log p(z\mid \theta)+\log p(D\mid z,\beta)) \right)\\
&=C\exp\left(E_{q(\theta)}\left[\log p(z\mid \theta) \right] +E_{q(\beta)}\left[\log p(D \mid z,\beta) \right] \right)\\
&=C\exp\left(E_{q( \theta)}\left[\log\prod_{d=1}^M\prod_{n=1}^{N_{d}} \theta_{dz_{dn}}) \right] +E_{q(\beta)}\left[\log\prod_{d=1}^M\prod_{n=1}^{N_{d}}\beta_{z_{dn}w_{dn}} \right] \right)\\
&=C\prod_{d=1}^M\prod_{n=1}^{N_d}\exp\left(E_{q( \theta)}\left[\log \theta_{dz_{dn}} \right]+E_{q(\beta)}\left[\log\beta_{z_{dn}w_{dn}} \right] \right)\\
&=C\prod_{d=1}^M\prod_{n=1}^{N_d}\exp\left(\int q( \theta)\log \theta_{dz_{dn}}d \theta+\int q(\beta)\log\beta_{z_{dn}w_{dn}}d\beta \right)\\
&=C\prod_{d=1}^M\prod_{n=1}^{N_d}\exp\left(\prod_{d'=1}^M\int Dir_k( \theta_{d'}\mid\gamma_{d'}) \log \theta_{dz_{dn}}d \theta_{d'}+\prod_{i=1}^{k}\int \log Dir_{V}(\beta_i\mid\lambda)\log\beta_{z_{dn}w_{dn}}d\beta_i \right)\\
&=C\prod_{d=1}^M\prod_{n=1}^{N_d}\exp\left(\int Dir_k( \theta_{d}\mid\gamma_{d}) \log \theta_{dz_{dn}}d \theta_{d}+\int \log Dir_{V}(\beta_{z_{dn}}\mid\lambda)\log\beta_{z_{dn}w_{dn}}d\beta_{z_{dn}} \right)
\end{align}

ここで確率密度がDirechlet分布の時の公式を導入します。
i番目変数の対数の期待は次のように書けます。
${\displaystyle \int Dir_k( \theta\mid\alpha)\log \theta_i d \theta = \Psi\left(\alpha_i \right)-\Psi\left(\sum_{i=1}^k\alpha_i \right) \tag{19} }$
但し、 $\Psi(x)$ はディガンマと呼ばれ、ガンマ関数のログの一階微分です。 $\Psi(x)=\frac{d\log\Gamma(x)}{dx}$

(17)を使いq(z)をさらに計算すると
${\displaystyle q(z)=C\prod_{d=1}^M\prod_{n=1}^{N_d}\exp\left(\Gamma\left(\gamma_{d z_{dn}} \right)-\Gamma\left(\sum_{i=1}^k\gamma_{di} \right) +\Gamma\left(\lambda_{z_{dn}w_{dn}} \right)-\Gamma\left(\sum_{w=1}^V\lambda_{z_{dn}w} \right) \right) }$
$q(z) =C\prod_{d=1}^M\prod_{n=1}^{N_d}\prod_{i=1}^kq(z_{dn}=i)$ とすると、
${\displaystyle q(z_{dn}=i)=\exp\left(\Psi\left(\gamma_{d i} \right)-\Psi\left(\sum_{j=1}^k\gamma_{dj} \right) +\Psi\left(\lambda_{iw_{dn}} \right)-\Psi\left(\sum_{w=1}^V\lambda_{iw} \right) \right) \tag{20} }$

(17),(18),(20)より

$\gamma_{di}$ , $\lambda_w$ をランダムに初期化した後に $q(z_{dn}=i)$ を求めて、その $q(z_{dn}=i)$ を使って $\gamma_{di}$ , $\lambda_w$ を更新する。これを繰り返す事で、適切な $\gamma_{di}$ , $\lambda_w$ , $q(z_{dn}=i)$ が求まり、そこから $\alpha, \eta$ が求まります。

12.パープレキシティー(Perplexity)

パラメータを推定するコードを書く前にモデルの性能の評価指標を紹介します。

Perplexityという指標です。テスト用の文書数を $M_{test}$ 、各文書の長さを $N_d^{test}$ 、文書セットを $D_{test}=({\bf w}_{1}^{test},{\bf w}_{2}^{test},...,{\bf w}_{M_{test}}^{test})$ ,文書を ${\bf w}_d^{test}=(w_{d1}^{test}, w_{d2}^{test},...,w_{dN_d^{test}}^{test})$ とすると次の式で表現されます。

${\displaystyle Perplexity(D_{test})=\exp\left(- \frac{\sum_{d=1}^{M_{test}}\sum_{n=1}^{N_d^{test}}\log p(w_{dn}^{test})}{\sum_{d=1}^{M_{test}}N_d^{test}} \right) \tag{21} }$

この式だけ見るとわかりにくいですが、ちょっと式変形をすると

\begin{align}
Perplexity(D_{test}) &= \left(\exp\left(-\sum_{d=1}^{M_{test}}\sum_{n=1}^{N_d^{test}}\log p(w_{dn}^{test}) \right) \right)^{\frac{1}{ \sum_{d=1}^{M_{test}}N_{d}^{test} }}\\
&= \left(\prod_{d=1}^{M_{test}}\prod_{n=1}^{N_d^{test}}\frac{1}{p(w_{dn}^{test})} \right)^{\frac{1}{ \sum_{d=1}^{M_{test}}N_{d}^{test} }}\tag{22}
\end{align}

となります。これは単語の生成確率 $p(w_{dn}^{test})$ の逆数の幾何平均になっていることがわかります。

そして単語の生成確率の逆数は選択肢の数を表しています。（例えば、 $p(w_{dn}^{test})=\frac{1}{1000}$ とかの場合は1000個の単語の中から選ぶ事を意味してるので。）
ですので、ランダム場合はPerprexityは出現単語数 $\sum_{d=1}^{M_{test}}N_{d}^{test}$ になり、完全に予測できるなら１になります。

ランダムに単語を生成するのではなく文書に現れる単語を限られた単語の中から選ぶ方が良いモデル（汎化性能が高い）だと言えるのでPerplexityが小さいほど良いモデル(汎化性能が高い)だと言えます。

実践

データセットと前処理（gensim使わないバージョン）

データセットの取得

データセットとして、livedoor ニュースコーパスを使います。
データセットをダウンロードして解凍しましょう。

wget https://www.rondhuit.com/download/ldcc-20140209.tar.gz
tar xvzf ldcc-20140209.tar.gz

前処理用モジュールをインストール

日本語は単語ごとに分ける作業（分かち書き）をしなければなりません。今回はMeCabという形態素解析ツールを使います。Macではbrewでインストール出来ます。

brew install mecab mecab-ipadic

MeCabは形態素解析に辞書を使っています。MeCabにも辞書は付いているのですが、日本語の新語や固有値表現に強いNEologdという辞書を使う事をオススメします。
インストールしましょう。

git clone --depth 1 https://github.com/neologd/mecab-ipadic-neologd.git
cd mecab-ipadic-neologd
./bin/install-mecab-ipadic-neologd -n

これらをPythonから使うためのモジュールをインストールします。

pip install mecab-python3

また、この後に使う必要なモジュールもインストールしときます。

pip install scipy numpy

前処理

準備が出来たのでPythonで前処理をしていきましょう。

▪️やること

　１. データの確認

　２. 分かち書き

　３. 必要な単語だけを抽出（ストップワード除外など）

　４. 数値化

まずは、必要モジュールをインポートします。

import itertools
import random
import MeCab
from urllib import request 
from pathlib import Path
import re
import numpy as np
from scipy.special import digamma

1.データの確認

データを"./text"のパスに解凍したとします。

doc_path = "./text/"
doc_dir = Path(doc_path)
dirs = [i for i in doc_dir.iterdir() if i.is_dir()]
print(dirs)
articles = [a for categ in dirs for a in categ.iterdir()]
print(articles[:3])
num_docs = len(articles)
print("# of docs:", num_docs)

出力

[PosixPath('text/movie-enter'),
 PosixPath('text/it-life-hack'),
 PosixPath('text/kaden-channel'),
 PosixPath('text/topic-news'),
 PosixPath('text/livedoor-homme'),
 PosixPath('text/peachy'),
 PosixPath('text/sports-watch'),
 PosixPath('text/dokujo-tsushin'),
 PosixPath('text/smax')]
[PosixPath('text/movie-enter/movie-enter-5978741.txt'), 
PosixPath('text/movie-enter/movie-enter-6322901.txt'), 
PosixPath('text/movie-enter/movie-enter-6176324.txt')]
# of docs: 7376

カテゴリーごとにディレクトリが別れていて、その下にtxtファイルのニュース記事が入っています。
記事の数は7376ですね。

記事の中身を確認します。

class Doc_manager():
    def __init__(self, docs):
        self.docs = docs
        
    def read_doc(self, doc_id):
        with self.docs[doc_id].open() as f:
            print(f.read())

dm = Doc_manager(articles)
dm.read_doc(0)
print("=================")
dm.read_doc(1)

出力

http://news.livedoor.com/article/detail/5978741/
2011-10-30T10:15:00+0900
【DVDエンター！】誘拐犯に育てられた女が目にした真実は、孤独か幸福か
　2005年11月から翌2006年7月まで読売新聞にて連載された、直木賞作家・角田光代による初の長編サスペンス『八日目の蝉』。2010年に檀れいと北乃きいの出演によりテレビドラマ化された同作が、2011年4月に永作博美と井上真央の出演によって映画化。そして、劇場公開から半年が過ぎた10月28日、DVD＆ブルーレイとなって発売されました。

八日目の蝉
　妻子ある男と愛し合い、その子を身ごもりながら、あきらめざるをえなかった女。彼女は同時に、男の妻が子供を産んだことを知る。その赤ん坊を見に行った女は、突発的にその子を連れ去り、逃避行を続けた挙句、小豆島に落ち着き、母と娘として暮らしはじめる。


不倫相手の子供を誘拐し、4年間育てた女
　永作博美が演じる野々宮希和子は、不倫相手の子を宿しながらも、彼の「いずれ妻と別れるから、それまで待ってくれ」という常套句を信じて、中絶。後遺症により、二度と子供を産めない身体となってしまいます。その後、不倫相手から彼の妻が出産したことを知らされ、別れを決意。最後に諦めをつけるため、彼らの生後6ヶ月の赤ん坊・恵理菜の顔を見た希和子でしたが、自分に笑顔で向けた恵理菜を見て、思わず誘拐。名前を変えて恵理菜を薫と名付けると、人目を避けて各地を転々とし、二人で幸せな時間を過ごしますが、辿り着いた最後の場所・小豆島で4年の逃避行に終止符を打ちます。


誘拐犯に育てられた女
　4歳になって実の両親と再会を果たした後も、世間から言われの無い中傷を受け、本当の両親との関係を築けないまま、21歳の大学生へと成長した恵理菜。過去と向き合うことを避けてきた恵理菜でしたが、劇団ひとりが演じる不倫相手・岸田孝史の子を宿し、ずっと憎み続けてきた希和子と同じ道を歩んでいることに気付いた彼女は、小池栄子が演じるルポライター・安藤千草と共に、4年間の逃亡生活を追憶する旅に出ます。希和子との幸せだった時間に触れながら、最終地・小豆島に辿り着いた恵理菜が見た真実とは？


八日目の蝉は幸せなのだろうか？
　蝉は俗説として、一生の大半を幼虫として地下で費やし、地上に出て羽化からわずか1週間程度で死ぬと言われています。八日目まで生き残ってしまった蝉が目にしたのは、孤独か、あるいは誰も目にすることのできなかった世界なのでしょうか。中絶によって二度と子供を埋めない身体になった希和子が、恵理菜と過ごした4年間の“八日目”は、希和子だけでなく、恵理菜にとっても幸せな時間だったのではないでしょうか。

　主題歌は、デビュー10年目に突入した2010年10月より、耳管開放症のため音楽活動を休止していた中島美嘉の復帰第一弾（通算33作目）シングル『Dear』。原作に深い感銘を受けた彼女が、本作のために提供した楽曲となっています。

・八日目の蝉 - 作品情報

八日目の蝉　通常版 [DVD]posted with amazlet at 11.10.29アミューズソフトエンタテインメント (2011-10-28)
売り上げランキング: 266
Amazon.co.jp で詳細を見る
■関連記事
・井上真央が逃避行？永作、森口、小池も頭を悩ます映画とは
=================
http://news.livedoor.com/article/detail/6322901/
2012-02-29T11:45:00+0900
藤原竜也、中学生とともにロケット打ち上げに成功
　「アンテナを張りながら生活をしていけばいい」

　2月28日、映画『おかえり、はやぶさ』（3月10日より公開）と文部科学省とのタイアップとして、千代田区立神田一橋中学校に通う中学三年生と“宇宙”をテーマにした特別授業を行った。本作で主演を務める藤原竜也がサプライズで登場し、イベントを盛り上げた。

　イベントの挨拶で奥村展三文部科学副大臣は「みなさんは大きな夢を持っているということで、実現するために、文部科学省も環境を作り応援していますので、チャレンジ精神で頑張ってください。」と参加した生徒たちにエールを送った。

　今回の特別授業は、2部制で行われた。第1部では、ロケットの中はどうなっているのか、発射した時の音の大きさなど、ロケットの不思議を日本宇宙少年団とJAXA（宇宙航空研究開発機構）が説明。参加した生徒は興味深く授業を受けていた。講義の最後に藤原が登場すると、何も知らなかった生徒から大きな歓声が上がり、会場はさらに盛り上がった。

　第2部では、藤原も参加し、生徒とともにアルコールロケットを発射させた。ロケットと同じ原理で飛ばすことで、さらに理解を深めるというもの。実際の燃料は水素と酸素だが、今回は、水素が危険を伴うためアルコールで代用。発射させたアルコールロケットが見事にくす玉に命中すると、中から“祝！　卒業「おかえり、はやぶさ」大ヒット祈願”という垂れ幕が登場した。参加した生徒132名との記念撮影も行われ、驚きと歓喜の中、イベントは終了した。

　藤原から今回のイベントについてコメントも届いている。


——『おかえり、はやぶさ』完成しましたね。
藤原：素敵な映画ができました。今日集まってくれているのは中学三年生ということで、卒業を控えて大変なこともたくさんあると思います。でも諦めず前に進んでください。


——久しぶりの学校だと思いますが、いかがですか？
藤原：学校ってこんなに寒かったっけ？（笑）でも、そんな寒い中を友達と遊んだ事を思いだし、興奮しています。

——藤原さんは宇宙に興味がありましたか？
藤原：かなり興味があります。はやぶさもリアルタイムで見たり調べたりしていましたし、宇宙だけでなく、生物や生命体にも興味がありました。往復7年間、60億キロの宇宙の旅を、はやぶさは帰ってきたんですけど、今回、本作に出演しなければわからなかった、JAXAの人達のすごく大変な苦労を知ることができました。僕も含め普通の人だったらこんな絶望的な出来事は諦めてしまと思いますが、JAXAの人達は、数センチ、数ミリの希望を奇跡的にキャッチすることで帰還させたわけですから、すごいことですよね。


——主演された役は夢と希望を持った役でしたが、中学三年生のみなさんと通じるところはありますか？
藤原：すごくあると思います。映画の中で「成功とは意欲を失わずに、失敗に次ぐ失敗を繰りかえすことである。」というウィンストン・チャーチルの言葉があるんですが、まさに多くの経験をして失敗をしてもらって、意欲を失わないで次に繋げるということは、通じるところだと思います。


——藤原さんの中学三年生の時の夢は何でしたか？
藤原：僕はずっとサッカーしかしていませんでした。勉強もろくにやらなくて、学校へは給食を食べに行っているだけでした（笑）。サッカー選手になりたかったんですが、ある時に演劇の世界に入ることになり、気が付いたら演劇の世界に引っ張られていました。みなさんもどこでどんな道が待っているかわからないので、アンテナを張りながら生活をしていけばいいと思います。あとは、自分を変えたりするのは人との出会いだと思うので、たくさんの人と出会って、たくさん恋愛もして（笑）。楽に楽しく過ごすことが大事ですよね。


——日本の宇宙開発プロジェクトに今後期待することは？
藤原：日本の開発技術はアジアで1位でなくてはいけないという大変な状況の中で、多くの国民に希望を与えてくれたはやぶさですから、はやぶさ2号機に関しても、もっともっと国民一人一人が応援していければ、活気がでるんじゃないかなと思います。


——最後に一言お願いします。
藤原：JAXAの奇跡の物語を実感できますし、もう一つのテーマの、家族や仲間の絆というところもありますので、たくさんのみなさんに観てもらって、もっと宇宙へ興味を持ってもらいたいです。そして夢へ向かって少し光を射してくれるような映画になっていればいいなと思っています。

　本作は、JAXAの協力のもと、2011年6月13日に約60億キロの飛行の末、地球へと帰還した小惑星探査機“はやぶさ”にまつわるさまざまなエピソードを3D映画化したもの。出演には、藤原を始め、杏、三浦友和、まえだまえだの前田旺志郎など各年代のキャストが勢揃いし、はやぶさと人々の冒険の旅を描く。

　映画『おかえり、はやぶさ』は、3月10日(土)より3D&2D同時公開。

・映画『おかえり、はやぶさ』 - 作品情報

【関連記事】
・藤原竜也、杏ら日本の俳優のスケールでは宇宙に行けない
・「はやぶさ」のグルメ登場！　うな重にカレーにケーキまで

1行目がURLで2行目が投稿日時になっているのがわかります。
これらはあまり意味が無いので、分かち書きの処理をする前に1行目と2行目を抜きます。

2.分かち書き

MeCabとNEologdを使ってみます。

mecab = MeCab.Tagger("-Ochasen -d /usr/local/lib/mecab/dic/mecab-ipadic-neologd/")
w = mecab.parse("認めたくないものだな。自分自身の若さ故の過ちというものを。")
print(w)

出力

認め	ミトメ	認める	動詞-自立	一段	連用形
たく	タク	たい	助動詞	特殊・タイ	連用テ接続
ない	ナイ	ない	助動詞	特殊・ナイ	基本形
もの	モノ	もの	名詞-非自立-一般
だ	ダ	だ	助動詞	特殊・ダ	基本形
な	ナ	な	助詞-終助詞
。	。	。	記号-句点
自分自身	ジブンジシン	自分自身	名詞-固有名詞-一般
の	ノ	の	助詞-連体化
若さ故の過ち	ワカサユエノアヤマチ	若さ故の過ち	名詞-固有名詞-一般
という	トイウ	という	助詞-格助詞-連語
もの	モノ	もの	名詞-非自立-一般
を	ヲ	を	助詞-格助詞-一般
。	。	。	記号-句点
EOS

上手く分けられてますね。

実はNEologdはかなり多くの分野の固有名詞や新語をカバーしているので次のような有名な（？）アニメのフレーズにも対応してます。

w = mecab.parse("今日も一日がんばるぞい")
print(w)

出力

今日も一日がんばるぞい	キョウモイチニチガンバルゾイ	今日も一日がんばるぞい	名詞-固有名詞-一般
EOS

３. 必要な単語だけを抽出（ストップワード除外など）

文書の中にはその文書の意味を表現しない単語も存在しています。
例えば、「あそこ」とか「あれ」や「わたし」や「あなた」などはどの文書にも同等に出てきそうですね。これらの単語はストップワードと呼ばれ除外処理をかけます。

日本語のストップワードは検索すればいくらでも出てきますし、HTTPリクエストで取得などでも取得できます。

res = request.urlopen("http://svn.sourceforge.jp/svnroot/slothlib/CSharp/Version1/SlothLib/NLP/Filter/StopWord/word/Japanese.txt")
stopwords = [line.decode("utf-8").strip() for line in res]
print(len(stopwords))
print(stopwords[:3])

出力

330
['あそこ', 'あたり', 'あちら']

330個のストップワードがありますね。
また日本語の特徴ですが、かなりの頻度で英単語も出てきます。なので英語のストップワードも使いましょう。

res = request.urlopen("http://svn.sourceforge.jp/svnroot/slothlib/CSharp/Version1/SlothLib/NLP/Filter/StopWord/word/English.txt")
stopwords += [line.decode("utf-8").strip() for line in res]
print(len(stopwords))
print(stopwords[-3:])

出力

910
["you've", 'z', 'zero']

ここまで出来たら、必要な単語だけを抽出するトークナイザーを作りましょう。

class Tokenizer:
    def __init__(self, stopwords, parser=None, include_pos=None, exclude_posdetail=None, exclude_reg=None):
    
        self.stopwords = stopwords
        self.include_pos = include_pos if include_pos else  ["名詞", "動詞", "形容詞"]
        self.exclude_posdetail = exclude_posdetail if exclude_posdetail else ["接尾", "数"]
        self.exclude_reg = exclude_reg if exclude_reg else r"$^"  # no matching reg
        if parser:
            self.parser = parser
        else:
            mecab = MeCab.Tagger("-Ochasen -d /usr/local/lib/mecab/dic/mecab-ipadic-neologd/")
            self.parser = mecab.parse
            

    def tokenize(self, text, show_pos=False):
        text = re.sub(r"https?://(?:[-\w.]|(?:%[\da-fA-F]{2}))+", "", text)    #URL
        text = re.sub(r"\"?([-a-zA-Z0-9.`?{}]+\.jp)\"?" ,"", text)  # xxx.jp 
        text = text.lower()
        l = [line.split("\t") for line in self.parser(text).split("\n")]
        res = [
            i[2] if not show_pos else (i[2],i[3]) for i in l 
                if len(i) >=4 # has POS.
                    and i[3].split("-")[0] in self.include_pos
                    and i[3].split("-")[1] not in self.exclude_posdetail
                    and not re.search(r"(-|−)\d", i[2])
                    and not re.search(self.exclude_reg, i[2])
                    and i[2] not in self.stopwords          
            ]
        return res
t = Tokenizer(stopwords, mecab.parse, exclude_reg=r"\d(年|月|日)")

処理としては
URLを除き、
英単語は全て小文字に変え、
分かち書きをして、
必要な品詞の単語だけを抽出し、
ニュース記事なので年月日は除いて、
ストップワードの単語を除いています。

必要な単語は扱うデータセットによって変わるのでトークナイザーは適宜作る必要があります。（これも抽出された単語などを見たりしてかなり試行錯誤しました。）

また、この先に実装するパラメータの推定のコードではメモリの事を考慮してないのであまり大きなデータは扱えません。（涙）
なので、今回は５０記事だけ扱いましょう。（ニュース記事レコメンドの実装では全部の記事を使います。）

articles = articles[:50]

文書を読み込んでトークナイザーで処理をしましょう。

docs = []
for a in articles:
    with a.open() as f:
        f.readline()
        f.readline()
        docs.append(t.tokenize(f.read()))

先に話したように1行目と2行目を抜いています。（これもデータセットによって変わることですね。）

４. 数値化

計算で扱えるように単語の数値化しましょう。

いろんなやり方がありますが、ここでは出現順に番号を振っていくシンプルな方法にします。（あとでもっと便利なモジュール（gensim）でのやり方も紹介します。）

vocab = set(w for d in docs for w in d)
word2id = dict(zip(vocab, itertools.count()))
id2word = dict(list(enumerate(vocab)))
corpus = []
for d in docs:
    corpus.append([word2id[w] for w in d])
random.shuffle(corpus)

学習（パラメータの推定）

変分法で(15),(16),(18)を導出して、推定方法を導いたのでコードを書きます。
まず、訓練データとテストデータに分けます。

test_size = int(len(corpus) * 0.2)
test_corpus = corpus[:test_size]
train_corpus = corpus[test_size:]

Perplexity

まずは評価するためにPerplexityのコードは次のようになりますね。

def get_per(corpus, alpha, eta, n_itr=100):
    perplexity = 0.0
    N = 0
    for d in corpus:
        N += len(d)
    for _ in range(n_itr):
        theta = np.array([np.random.dirichlet(a) for a in alpha])
        beta = np.array([np.random.dirichlet(e) for e in eta.T])
        m = np.inner(theta, beta.T)
        log_p = 0.0
        for i, d in enumerate(corpus):
            log_p += np.log(m[i][d]).sum()
        perplexity += np.exp(-log_p/N)
    perplexity = perplexity/n_itr
    return perplexity

テスト用のコーパスと $\alpha,\eta$ を入れるとperplexityを返します。

推定のコード

訓練用の文書数、語彙数、トピック数を設定します。

M = len(train_corpus)
V =  len(vocab)
k = 10

トピック数はハイパーパラメータなので今回は適当に10に設定します。

そして、推定のコードですが、愚直に書くと以下のようになります。

gamma_ = np.random.rand(M, k)
lambda_ = np.random.rand(V, k)
q_ = np.random.rand(M,V,k)

for itr in range(50):
    
    for d in range(M):
        doc = train_corpus[d]
        N_d = len(doc)
        for n in range(N_d):
            gamma_sum = gamma_.sum(axis=1)
            lambda_sum = lambda_.sum(axis=0)
            w = int(doc[n])

            q_[d,w] = np.exp(digamma(gamma_[d]) - digamma(gamma_sum)[d] + digamma(lambda_[w]) - digamma(lambda_sum))
            q_ = q_/q_.sum()
            gamma_[d] += q_.sum(axis=1)[d]
            lambda_[w] += q_.sum(axis=0)[w]
            

    alpha = gamma_ - q_.sum(axis=1)
    eta = lambda_ - q_.sum(axis=0)
    
    perplexity = get_per(test_corpus, alpha, eta, n_itr=200)
    print(itr, ": ", perplexity)

コードはすごい短いですがちゃんと学習してることがわかります。
出力

0 :  5674.503062673437
1 :  5584.766914247157
2 :  5511.157678168981
3 :  5458.629214717671
4 :  5418.940672207456
5 :  5379.257701873946
6 :  5328.143392841107
7 :  5297.88857102558
8 :  5264.242833398944
9 :  5235.628752569887
10 :  5199.703462080557
11 :  5156.645192115948
12 :  5123.23351388193
13 :  5092.54674403159
14 :  5050.536784773745
15 :  5018.391691114887
16 :  4985.750386617771
17 :  4945.832561518353
18 :  4906.42566531194
19 :  4868.334885573498
20 :  4842.070715295144
21 :  4802.508475658399
22 :  4753.586082804895
23 :  4719.6031370937
24 :  4682.7992544631115
25 :  4645.03757931315
26 :  4604.155215611624
27 :  4567.416380723154
28 :  4532.778039892515
29 :  4490.754145540746
30 :  4454.957132518847
31 :  4424.7972241131565
32 :  4384.09769409566
33 :  4357.054906748676
34 :  4326.873841218807
35 :  4292.199106543804
36 :  4270.729563402634
37 :  4239.36314904691
38 :  4218.57396129725
39 :  4203.02290208137
40 :  4185.588207515016
41 :  4178.228522783321
42 :  4171.95975328867
43 :  4159.8373245942
44 :  4161.101756829013
45 :  4170.555677440166
46 :  4173.87798817788
47 :  4191.880166832307
48 :  4210.302445744775
49 :  4227.922383412469

また、テストデータの出現単語数を調べます。

N = 0
for d in test_corpus:
        N += len(d)
print(N)

出力

ランダムだとPerplexityは出現単語数と一致する事を思い出すと、出現単語数より小さくなっているのでちゃんと学習できたことがわかりますね。
途中からPerplexityが大きくなって過学習をしているので本来は途中で学習をやめるべきでした。

上手く学習できているのでこれを使ってニュース記事レコメンドを作りたいのですが、この推定法はあまり精度が出ないことが知られています。*12
また、同じ変分ベイズを使いオンライン学習を可能にしたOnlineLDAという実装*13もあり、そちらの方が精度が良いです。
さらに実装に当たってはメモリのことや速度のことも考えなければなりません。
なのでだいたいどういう事をしているのか理解は出来たと思うので、ここからは人類の集合知の恩恵を受ける事にしてgensimというライブラリを使います。（gensimのLDAはOnlineLDA実装です。）

gensim

公式サイト
radimrehurek.com

800以上の商用・アカデミックアプリケーションで使われているベクトル空間モデル、トピックモデル用のPythonライブラリです。
公式サイトにはtopic modeling for humansと書いてますが、トピックモデル以外の自然言語処理に関わる様々なアルゴリズムを試すことが出来ます。（word2vec, doc2vec,fasttextなどなど）

また、オライリーの『ハイパフォーマンスPython』の中で開発者のŘehůřekさんがgensimの開発の際(主にword2vec)の最適化についてインタビューを受けているので興味ある人は読んでみてください。

インストールはpipで出来ます。

pip install gensim

ニュース記事レコメンド

livedoor ニュースコーパスのニュース記事1つを選んだ時に似た記事をレコメンドするエンジンを作ります。
gensimを使います。

必要なモジュールのインポート

from urllib import request 
import logging
from pathlib import Path
import numpy as np
import re
import MeCab
import random
from gensim import corpora, models

前処理（with gensim）

数値化する前までは基本的には上で紹介した方法と同じです。

res = request.urlopen("http://svn.sourceforge.jp/svnroot/slothlib/CSharp/Version1/SlothLib/NLP/Filter/StopWord/word/Japanese.txt")
stopwords = [line.decode("utf-8").strip() for line in res]
res = request.urlopen("http://svn.sourceforge.jp/svnroot/slothlib/CSharp/Version1/SlothLib/NLP/Filter/StopWord/word/English.txt")
stopwords += [line.decode("utf-8").strip() for line in res]

class Tokenizer:
    def __init__(self, stopwords, parser=None, include_pos=None, exclude_posdetail=None, exclude_reg=None):
    
        self.stopwords = stopwords
        self.include_pos = include_pos if include_pos else  ["名詞", "動詞", "形容詞"]
        self.exclude_posdetail = exclude_posdetail if exclude_posdetail else ["接尾", "数"]
        self.exclude_reg = exclude_reg if exclude_reg else r"$^"  # no matching reg
        if parser:
            self.parser = parser
        else:
            mecab = MeCab.Tagger("-Ochasen -d /usr/local/lib/mecab/dic/mecab-ipadic-neologd/")
            self.parser = mecab.parse
            

    def tokenize(self, text, show_pos=False):
        text = re.sub(r"https?://(?:[-\w.]|(?:%[\da-fA-F]{2}))+", "", text)    #URL
        text = re.sub(r"\"?([-a-zA-Z0-9.`?{}]+\.jp)\"?" ,"", text)  # xxx.jp 
        text = text.lower()
        l = [line.split("\t") for line in self.parser(text).split("\n")]
        res = [
            i[2] if not show_pos else (i[2],i[3]) for i in l 
                if len(i) >=4 # has POS.
                    and i[3].split("-")[0] in self.include_pos
                    and i[3].split("-")[1] not in self.exclude_posdetail
                    and not re.search(r"(-|−)\d", i[2])
                    and not re.search(self.exclude_reg, i[2])
                    and i[2] not in self.stopwords          
            ]
        return res
t = Tokenizer(stopwords + ["…。"] , mecab.parse, exclude_reg=r"\d(年|月|日)")

doc_path = "./text/"
doc_dir = Path(doc_path)
dirs = [i for i in doc_dir.iterdir() if i.is_dir()]
articles = [a for categ in dirs for a in categ.iterdir()]
random.shuffle(articles)


class Doc_manager():
    def __init__(self, docs):
        self.docs = docs
        
    def read_doc(self, doc_id):
        with self.docs[doc_id].open() as f:
            print(f.read())

dm = Doc_manager(articles)

docs = []
for a in articles:
    with a.open() as f:
        f.readline()
        f.readline()
        docs.append(tokenize(f.read()))

ここからgensimを使います。gensimにはcorpora.Dictionaryという単語とIDのマッピングを扱う便利なツールが用意されています。

d = corpora.Dictionary(docs)

使い方は以下の様になります。

print(d[1000])
print(d.token2id["長い"])
print(d.doc2bow(["長い","長い","短い"]))

出力

長い
1000
[(1000, 2), (4362, 1)]

IDが1000の単語を取得したいときはインデックスでアクセスすればよくて、"長い"という単語のIDを取得したい場合はtoken2idが使えます。また、doc2bowを使ってBOWを取得することもできます。(ID, 出現回数)の形です。

また、フィルター機能もあります。ストップワードやトークナイザーの処理で取り除くことが出来なかった不要な単語を除去できます。

d.filter_extremes(no_below=5, no_above=0.2)
d.compactify()

使われいる文書の数がno_belowより少ない単語を無視し、no_aboveの割合以上の文書に出てくる単語を無視しています。
また、compactifyでIDを振り直してコンパクトにしてます。

LDAの学習に使うコーパスを作ります。

corpus = [d.doc2bow(w) for w in docs]
test_size = int(len(corpus) * 0.1)
test_corpus = corpus[:test_size]
train_corpus = corpus[test_size:]

ここまで出来たらLDAの学習が出来ます。

LDAの学習

学習状況を見るためにlogの設定をする事をオススメします。

logging.basicConfig(format='%(message)s', level=logging.INFO)

トピック数を適当に50に設定して学習を開始します。

lda = models.ldamodel.LdaModel(corpus=corpus, id2word=d, num_topics=50, passes=10)

出力(ログの)

using symmetric alpha at 0.02
using symmetric eta at 0.02
using serial LDA version on this node
running online (multi-pass) LDA training, 50 topics, 10 passes over the supplied corpus of 6639 documents, updating model once every 2000 documents, evaluating perplexity every 6639 documents, iterating 50x with a convergence threshold of 0.001000
PROGRESS: pass 0, at document #2000/6639
merging changes from 2000 documents into a model of 6639 documents
topic #20 (0.020): 0.005*"映画" + 0.003*"iphone" + 0.003*"気持ち" + 0.002*"写真" + 0.002*"いく" + 0.002*"対応" + 0.002*"チェック" + 0.002*"スマートフォン" + 0.002*"仕事" + 0.002*"相手"
topic #22 (0.020): 0.004*"結婚" + 0.003*"利用" + 0.003*"しまう" + 0.003*"思う" + 0.003*"アプリ" + 0.003*"更新" + 0.003*"サービス" + 0.002*"浮気" + 0.002*"ください" + 0.002*"現在"
topic #15 (0.020): 0.007*"ご" + 0.005*"機能" + 0.005*"スマートフォン" + 0.004*"ください" + 0.004*"対応" + 0.004*"写真" + 0.004*"当選" + 0.003*"応募" + 0.003*"映画" + 0.003*"プレゼント"
topic #31 (0.020): 0.003*"対応" + 0.003*"映画" + 0.002*"flash" + 0.002*"人気" + 0.002*"max" + 0.002*"スマートフォン" + 0.002*"ユーザー" + 0.002*"機能" + 0.002*"画面" + 0.002*"搭載"
topic diff=25.199308, rho=1.000000
PROGRESS: pass 0, at document #4000/6639
merging changes from 2000 documents into a model of 6639 documents
topic #4 (0.020): 0.021*"アプリ" + 0.006*"android" + 0.006*"表示" + 0.005*"max" + 0.005*"画面" + 0.005*"登録" + 0.004*"エスマックス" + 0.004*"利用" + 0.004*"store" + 0.004*"更新"
topic #8 (0.020): 0.009*"肌" + 0.008*"ソフトバンク" + 0.005*"ゴルフ" + 0.004*"選手" + 0.003*"ファン" + 0.003*"美人" + 0.003*"思う" + 0.003*"いく" + 0.003*"出" + 0.003*"ゴルファー"
topic #48 (0.020): 0.009*"映画" + 0.006*"結婚" + 0.005*"くれ" + 0.003*"言わ" + 0.003*"仕事" + 0.003*"気持ち" + 0.003*"心" + 0.003*"公開" + 0.003*"作品" + 0.003*"監督"
topic #39 (0.020): 0.006*"男性" + 0.005*"声" + 0.004*"知っ" + 0.004*"得" + 0.004*"てる" + 0.004*"結婚" + 0.003*"思う" + 0.003*"イベント" + 0.003*"韓国" + 0.003*"好き"
topic #20 (0.020): 0.004*"映画" + 0.003*"気持ち" + 0.003*"仕事" + 0.003*"相手" + 0.003*"いく" + 0.002*"写真" + 0.002*"女子" + 0.002*"しまう" + 0.002*"特集" + 0.002*"発言"
topic diff=3.696819, rho=0.707107
~~~(略)~~~

この様なログが出力され、学習途中のパラメータやトピックを確認できます。
このデータ量だったのでMac book Pro（プロセッサ Corei7 メモリ16G）で数分程度で学習は終わりました。
学習が終わったらテストコーパスでPerplexityを確認しましょう。

N = sum(count for doc in test_corpus for id, count in doc)
print("N: ",N)

perplexity = np.exp2(-lda.log_perplexity(test_corpus))
print("perplexity:", perplexity)

出力

N:  139057
perplexity: 1855.2785790213302

出現単語数Nに比べて非常に小さな値になっているので良いモデルになっていることが確認できます。

トピックを確認して見ましょう。（10個ぐらい）

def get_topic_words(topic_id):
    for t in lda.get_topic_terms(topic_id):
        print("{}: {}".format(d[t[0]], t[1]))
for t in range(10):
    print("Topic # ",t)
    get_topic_words(t)
    print("\n")

出力

Topic #  0
ヒーロー: 0.023730993270874023
公開: 0.015601863153278828
最強: 0.015375325456261635
アベンジャーズ: 0.014256509020924568
人類: 0.011246700771152973
記録: 0.010951797477900982
地球: 0.009402085095643997
映画: 0.007777830585837364
キャプテン・アメリカ: 0.0076071820221841335
世界: 0.0074112629517912865


Topic #  1
仕事: 0.01630249060690403
結果: 0.010680487379431725
考え: 0.008862967602908611
会社: 0.008609889075160027
調査: 0.007379303686320782
必要: 0.005950006190687418
年収: 0.005934941116720438
ビジネス: 0.005180467385798693
いく: 0.0046653421595692635
高い: 0.0045888046734035015


Topic #  2
肌: 0.06868039816617966
韓国: 0.02120852842926979
成分: 0.01797901839017868
配合: 0.016065062955021858
ケア: 0.015182935632765293
コスメ: 0.01265209261327982
geforce gtx: 0.01075231097638607
毛穴: 0.01063121110200882
クリーム: 0.010575288906693459
スキンケア: 0.00983455590903759


Topic #  3
転職: 0.05346670374274254
livedoor: 0.02633664198219776
仕事: 0.023270638659596443
求人: 0.020375752821564674
悩み: 0.019349485635757446
会社: 0.017803464084863663
活動: 0.014538266696035862
コンテンツ: 0.013969127088785172
説教: 0.012373720295727253
判断: 0.011847401969134808


Topic #  4
アプリ: 0.0694742500782013
android: 0.02808075211942196
max: 0.016350433230400085
画面: 0.015707241371273994
エスマックス: 0.01357377041131258
表示: 0.01272848155349493
iphone: 0.012610442005097866
無料: 0.012191498652100563
twitter: 0.010832356289029121
タップ: 0.010797367431223392


Topic #  5
pc: 0.015194461680948734
搭載: 0.014297448098659515
対応: 0.014269378036260605
製品: 0.012111667543649673
機能: 0.010044978931546211
可能: 0.009972632862627506
接続: 0.00836364645510912
usb: 0.006858081556856632
シリーズ: 0.006152425426989794
スマートフォン: 0.005825271364301443


Topic #  6
デジ: 0.018907519057393074
機能: 0.01732938550412655
デジタル: 0.014969095587730408
ユーザー: 0.010697913356125355
サービス: 0.010371265932917595
パソコン: 0.009319713339209557
提供: 0.009241793304681778
使える: 0.009118852205574512
機器: 0.008886301890015602
現在: 0.0088787991553545


Topic #  7
映画: 0.04781694337725639
公開: 0.020408974960446358
作品: 0.018162159249186516
監督: 0.01602139323949814
本作: 0.013156397268176079
演じる: 0.007427051197737455
特集: 0.007043853402137756
movie: 0.006705742795020342
主演: 0.005962018854916096
大: 0.0059361811727285385


Topic #  8
て: 0.010121898725628853
監督: 0.009650022722780704
sports: 0.009441154077649117
watch: 0.008757323957979679
ゴルフ: 0.0084562161937356
放送: 0.007622931618243456
ボール: 0.007172265090048313
チーム: 0.006855555344372988
やっ: 0.0067366985604166985
練習: 0.006228393409401178


Topic #  9
ツイート: 0.024701008573174477
ツイッター: 0.02284015715122223
北朝鮮: 0.014550372026860714
tbs: 0.008325724862515926
ローラ: 0.008248904719948769
松井: 0.007412313483655453
言い訳: 0.006594712845981121
内田: 0.006575769279152155
てる: 0.0060353041626513
不倫: 0.005640488117933273

"単語:割合"という形式で出力してます。それぞれのトピックが近い意味の単語分布になっている様に見えますね。

また、文書のトピック分布は次の様に確認できます。

topics = sorted(lda.get_document_topics(corpus[0]), key=lambda t:t[1], reverse=True)
for t in topics[:10]:
    print("{}: {}".format(t[0], t[1]))

出力

10: 0.4286927580833435
16: 0.19554442167282104
28: 0.09656607359647751
33: 0.05863435938954353
44: 0.047012779861688614
5: 0.04349694028496742
1: 0.03415320813655853
15: 0.028384555131196976
13: 0.02286113239824772
41: 0.01004168763756752

これも"トピックの番号:割合"という形式で出力してます。
主にトピック10で構成さていて、そのあとにトピック16、28と続いてますね。
このトピックの単語分布も確認しましょう。

for t in topics[:10]:
    print("Topic # ",t[0])
    get_topic_words(t[0])
    print("\n")

出力

Topic #  10
搭載: 0.02390816994011402
スマートフォン: 0.021327851340174675
対応: 0.021220998838543892
nttドコモ: 0.012328347191214561
機能: 0.011351358145475388
モデル: 0.011222900822758675
max: 0.011020414531230927
cpu: 0.009783013723790646
カメラ: 0.009003721177577972
ディスプレイ: 0.00869847647845745


Topic #  16
htc: 0.021657699719071388
line: 0.013200951740145683
子供: 0.009489757940173149
老人ホーム: 0.007789401803165674
妊娠: 0.007769452873617411
detail: 0.006128225941210985
脳: 0.00582770723849535
年金: 0.005326862912625074
ジャニーズ: 0.005224371794611216
処分: 0.004653443582355976


Topic #  28
スマートフォン: 0.02225065976381302
ソフトバンク: 0.022145671769976616
max: 0.022095773369073868
ドコモ: 0.015159054659307003
sc: 0.013579449616372585
エスマックス: 0.01169624924659729
購入: 0.011320103891193867
対応: 0.010671828873455524
galaxy s: 0.010225505568087101
キャンペーン: 0.009902272373437881


Topic #  33
撮影: 0.07201525568962097
動画: 0.04066493734717369
カメラ: 0.038062382489442825
写真: 0.023346638306975365
レンズ: 0.011216390877962112
映像: 0.01105312816798687
機能: 0.01095964852720499
ニコニコ動画: 0.010317344218492508
ビデオ: 0.007901370525360107
画像: 0.007722283713519573


Topic #  44
画面: 0.02682238444685936
表示: 0.02116880752146244
facebook: 0.016731226816773415
設定: 0.01661299169063568
ニュース: 0.012996634468436241
得: 0.012161778286099434
知っ: 0.011591647751629353
クリック: 0.01136905886232853
入力: 0.011217259801924229
便利: 0.011154274456202984


Topic #  5
pc: 0.015194461680948734
搭載: 0.014297448098659515
対応: 0.014269378036260605
製品: 0.012111667543649673
機能: 0.010044978931546211
可能: 0.009972632862627506
接続: 0.00836364645510912
usb: 0.006858081556856632
シリーズ: 0.006152425426989794
スマートフォン: 0.005825271364301443


Topic #  1
仕事: 0.01630249060690403
結果: 0.010680487379431725
考え: 0.008862967602908611
会社: 0.008609889075160027
調査: 0.007379303686320782
必要: 0.005950006190687418
年収: 0.005934941116720438
ビジネス: 0.005180467385798693
いく: 0.0046653421595692635
高い: 0.0045888046734035015


Topic #  15
商品: 0.017195843160152435
イベント: 0.012727107852697372
ビデオsalon: 0.012197132222354412
開催: 0.010742572136223316
デザイン: 0.009651359170675278
チェック: 0.008599182590842247
ブランド: 0.007262687664479017
新: 0.007121855393052101
販売: 0.006953767500817776
限定: 0.006405428983271122


Topic #  13
充電: 0.035104893147945404
iphone: 0.028389062732458115
バッテリー: 0.026957286521792412
ケース: 0.021976225078105927
ipad: 0.015676002949476242
容量: 0.013837297447025776
スマホ: 0.011868351139128208
大: 0.011050853878259659
装着: 0.01052774116396904
イケショップ: 0.010489579290151596


Topic #  41
更新: 0.10627567023038864
ソフトウェア: 0.07545258849859238
ください: 0.028703970834612846
ダウンロード: 0.015537954866886139
ご: 0.014859003946185112
表示: 0.014070549048483372
設定: 0.010349449701607227
行う: 0.01013778056949377
操作: 0.009964043274521828
実施: 0.009850624948740005

確認してみましょう。

dm.read_doc(0)

出力

http://news.livedoor.com/article/detail/6668229/
2012-06-18T11:55:00+0900
海外向けSIMフリーモデル「HTC One V T320e」を使ってみよう！ソフトバンクの「HTC Desire X06HT」と比較した【レビュー】
およそ2年で何が変わった？Desireとの比較 

ローエンドからミドルエンドユーザーをターゲットにしたHTC製の「HTC One V T320e」（以下、HTC One V）は、Android 4.0.3(開発コード名：IceCream Sandwich；ICS)を採用したスマートフォンで、グローバル市場では4月に発売されているが日本向けには発売されていない。

前回は外観や同梱品をチェックしたが、今回は、およそ2年前にソフトバンクから発売された「HTC Desire X06HT」(以下、X06HT)と比較してみる。外観やディスプレイをチェックし、X06HTが発売してから2年経過して何が変わったかを見ていこう。


本体正面。左がHTC One V、右がX06HT


本体背面
どちらもディスプレイサイズは約3.7インチと同等のため本体サイズも近い。X06HTが全体的に丸みを帯びたラウンドフォルムのため、並べて比較するとHTC One Vはスクエアなデザインに見えるが、単体で持ってみるとHTC One Vも角の取れたデザインや、しゃくれた部分のカーブなど曲線ラインを多用しており、角ばったイメージはほとんどしない。



本体向かって左側面（画像上）と右側面（画像下）
左右の側面を比較すると色々な違いが分かる。まずは、X06HTでは左側面に搭載されていた＋−キー(上下キー)が、HTC One Vでは右側面に搭載されている。microUSB端子もHTC One Vでは左側面に搭載されている。

そして、本体の高さがHTC One Vでは大きくなっており、厚みはHTC One Vが薄くなっていることも分かる。実際の厚みはX06HTが11.9mm、HTC One Vが9.24mm、重量もX06HTは約135gでHTC One Vは約115gとなっており、薄型化・軽量化され手に持った際の印象が全く異なる。



本体向かって上部側面（画像上）と下部側面（画像下）
上下の側面も全て変更されている。上部側面の電源キーと3.5mmイヤホンジャックの位置が逆になっているほか、X06HTではディスプレイ上部に搭載されていたお知らせ用のLEDランプがHTC One Vでは上部側面に搭載されている。

このLEDランプは充電中、充電完了、不在着信、メールなどの通知時に光る。内容としてはどちらも同じ役割を担っているが位置と形状が変わった。



背面のカメラ部分。手前がHTC One Vで奥がX06HT
カメラの位置や周囲のデザインも変わりよりスタイリッシュさが増したといえる。HTC One Vのカメラ位置は本体背面向かって左側に寄せられており、これは右側の上部にある3.5mmイヤホンジャックにイヤホンを挿した際にケーブルがカメラにかからないようなっているため、イヤホンをつないだままでも撮影がしやすい。

反面、横撮りをする際に左手の指の位置を考えないと写り込んでしまう点がネックだ。縦撮りがメインの場合は特に気にならないだろう。

また、X06HTでは上部に搭載されているスピーカーが、HTC One Vでは下部のしゃくれた部分に搭載されている。



本体正面下部を比較。手前がHTC One Vで奥がX06HT
デザイン的に最も違いが分かる本体正面の下部。X06HTではディスプレイ直下にホーム、menu、バック、Google検索の物理キーに加え、光学ジョイスティックを備えているが、HTC One Vはバック、ホーム、タスクのセンサーキーのみとなっている。

Androidのバージョンが異なる点も変更の要因でもあるが、できれば物理キー、光学ジョイスティックは継承して欲しところだ。特に光学ジョイスティックは非常に便利で「これがあるからX06HTを使っている！」というユーザーも少なくない。Android端末の主流ではないが、ブラウジング、メールなどの操作において利用価値が高いのは間違いない。



ディスプレイの比較。左がHTC One V、右がX06HT
X06HTは有機ELを搭載しており、非常に鮮やかな表示をするが、HTC One Vではさらに明るく綺麗なディスプレイになっている。解像度はどちらも480×800ドットのワイドVGA。画像では分かり難いがHTC One VはX06HTに比べ、液晶パネルが前に出てきているため明るく綺麗に見える。



明るさを一番低くして比較


明るさを一番低くしたまま角度を付けて比較
明るさ調整で一番暗い状態にして比較したところその違いがよく分かった。有機ELからTFT液晶に変更されているが、ディスプレイの表示においてはHTC One Vはとても明るく鮮やかになっている。


X06HTは、当時としてはハイスペックでありながらスタイリッシュなデザインだったが、それでもHTC One Vと比べてしまうとぽってり感が否めない。逆にHTC One Vは、より洗練されたデザインと言えるだろう。


記事執筆：2106bpm（つとむびーぴーえむ）

■関連リンク
・エスマックス（S-MAX）
・エスマックス（S-MAX） smaxjp on Twitter
・海外向けSIMフリーモデル「HTC One V T320e」を使ってみよう！写真で外観チェック【レビュー】 - S-MAX - ライブドアブログ
・HTCの新グローバル端末「HTC One」シリーズ3機種を実際に触ってみた「HTC One V編」【レポート】 - S-MAX - ライブドアブログ
・HTC Nippon、グローバルモデル「HTC One」シリーズの説明会を開催！日本への投入やKDDIとの協業については言及せず - S-MAX - ライブドアブログ
・HTC、Android 4.0 ICS搭載「HTC Oneシリーズ」を4機種発表！One X、One XL、One S、One Vが登場 - S-MAX - ライブドアブログ
・【最近のオススメ「Androidアプリ」特集：2012年6月4〜10日編】 - S-MAX - ライブドアブログ
・HTC One V Product Overview(HTC Corporation.)
・HTC 日本

予測通りスマホのレビューでした。文書を形成するトピック分布の方も良さそうですね。

可視化

全体的に問題無いか確認するために可視化します。
文書をトピックによって張られるベクトル空間（今回は５０次元）だとしてそれを次元圧縮で３次元と２次元にして確認して見ましょう。
(以降、トピックによって張られるベクトル空間のことをトピック空間と呼ぶ)
先ずは全ての文書のトピックを取得しましょう。

all_topics = lda.get_document_topics(corpus, minimum_probability=0)
<||
試しに0番目の文書のトピックを見ましょう。
>|python|
print(all_topics[0])

出力

[(0, 4.6838402e-05),
 (1, 0.03413247),
 (2, 4.6838402e-05),
 (3, 0.0029260195),
 (4, 0.009185041),
 (5, 0.043502126),
 (6, 4.6838402e-05),
 (7, 4.6838402e-05),
 (8, 4.6838402e-05),
 (9, 4.6838402e-05),
 (10, 0.42869237),
 (11, 4.6838402e-05),
 (12, 4.6838402e-05),
 (13, 0.02286147),
 (14, 4.6838402e-05),
 (15, 0.028384523),
 (16, 0.19554703),
 (17, 4.6838402e-05),
 (18, 4.6838402e-05),
 (19, 0.0042972392),
 (20, 4.6838402e-05),
 (21, 4.6838402e-05),
 (22, 4.6838402e-05),
 (23, 4.6838402e-05),
 (24, 4.6838402e-05),
 (25, 4.6838402e-05),
 (26, 4.6838402e-05),
 (27, 4.6838402e-05),
 (28, 0.096573636),
 (29, 4.6838402e-05),
 (30, 0.003768291),
 (31, 4.6838402e-05),
 (32, 4.6838402e-05),
 (33, 0.058640447),
 (34, 4.6838402e-05),
 (35, 0.006743891),
 (36, 0.006086506),
 (37, 4.6838402e-05),
 (38, 4.6838402e-05),
 (39, 4.6838402e-05),
 (40, 4.6838402e-05),
 (41, 0.010041841),
 (42, 4.6838402e-05),
 (43, 4.6838402e-05),
 (44, 0.047024604),
 (45, 4.6838402e-05),
 (46, 4.6838402e-05),
 (47, 4.6838402e-05),
 (48, 4.6838402e-05),
 (49, 4.6838402e-05)]

出力は（トピックの番号,割合）ですが、これを(基底の番号,成分)とみなすことでトピック空間を作ります。

可視化にはEmbedding Projectorを使います。
サイト：
projector.tensorflow.org

ブラウザ上からデータをアップロードして簡単に次元圧縮ができる便利なサイトです。

まずはアップロードするためのtsvファイルを作ります。

with open('doc_lda_tensor.tsv','w') as w:
    for doc_topics in all_topics:
        for topics in doc_topics:
            w.write(str(topics[1])+ "\t")
        w.write("\n")

また、メタデータを作りそれぞれのデータにタイトルをつけることが出来るのですが、元々のデータセットが記事のテーマごとにディレクトリに分けられていたので、タイトルにはテーマ名をつけてトピックが元のテーマをちゃんと再現できているか確認します。

meta = [str(a).split("/") for a in articles]
with open('doc_lda_metadata.tsv','w') as w:
    w.write('Titles\tGenres\n')
    for m in meta:
        w.write("%s\t%s\n" % (m[1].split("-")[0], m[1]))

Embedding Projectorを開いて左側の"Load data"ボタンからそれぞれのtsvファイルをアップロードしましょう。
PCAの３次元圧縮では次のような感じになりました。

f:id:tdualdir:20180405192735g:plain — 図6.３次元圧縮

t-SNEの２次元圧縮では次のようになりました。

f:id:tdualdir:20180406153810p:plain — 図7.２次元圧縮

テーマごとに別れていますね。
なので生成したトピックは単語からちゃんとテーマを捉えることが出来ている事がわかりました。

ニュース記事レコメンドの作成

実はgensimにはsimilaritiesというメソッドがあるのでここまでくればサクッと作れます。

from gensim import similarities
doc_index = similarities.docsim.MatrixSimilarity(lda[corpus])

これでコサイン類似度*14を保持したオブジェクトが作られたので、記事のインデックスを指定することでトピック空間のベクトルが取得できます。

target_article = 0
vec_lda = lda[target_article]

vec_ldaは先ほどのall_topic[0]の値と同じです。
__getitem__でこのベクトルを指定することで類似度を取得できます。*15

s = doc_index.__getitem__(vec_lda)
s = sorted(enumerate(s), key=lambda t: t[1], reverse=True) 
s[:10]

出力

[(0, 0.99995905),
 (1881, 0.95702314),
 (6841, 0.92270225),
 (935, 0.9120116),
 (5687, 0.9099416),
 (2380, 0.90439415),
 (706, 0.90099066),
 (6336, 0.89967924),
 (20, 0.8994651),
 (528, 0.8989129)]

(記事のインデックス,類似度)の形式で出力してます。類似度が大きい順にソートして上から10個まで表示しています。
一番上は入力したベクトルなので一番類似しているのは1881で、6841,935,...と続く結果になっています。
これらのニュース記事を見て見ましょう。

for doc_id in [1881,6841,935]:
    with articles[doc_id].open() as f:
        print("#", doc_id)
        print(f.read())
        print("===========")

出力

# 1881
http://news.livedoor.com/article/detail/6656576/
2012-06-14T09:55:00+0900
海外向けSIMフリーモデル「HTC One V T320e」を使ってみよう！写真で外観チェック【レビュー】
HTC製のコンパクトスマートフォン「HTC One V T320e」をチェック！ 

「HTC One V T320e」（以下、HTC One V）は、今年の2月27日にバルセロナ(スペイン)で開催された「Mobile World Congress 2012(MWC2012)」において、HTCがグローバルモデルの新製品「HTCOneシリーズ」として発表したモデルの1つ。3月27日にはHTC Nipponが、このHTC Oneシリーズの製品説明会を都内で開催しているが、日本向けには発売していない。

グローバル市場では4月に発売されているHTC One Vだが、ネット通販では販売価格が2万円台と既に大幅に値下がりしてきているので入手してみた。数回に渡ってこのHTC One Vのレビューを行っていく。まずは外観をチェックしてみる。


パッケージ表面(左)と裏面(右)


パッケージ裏面の表記


ご開帳
パッケージに記載されている仕様は以下の通り。
Model T320e
CPU 1GHz
Platform Android with HTC Sense
Memory 512MB RAM, Storage:4GB Total / up to 1.1GB Available
Display and sound 3.7-inch touch screen, Beats Audio support
Camera 5 megapixel camera, F2.0 28mm lens, auto focus, LED flash, 720p HD video recording
Connectivity 3.5mm stereo audio jack and microUSB, Bluetooth, Wi-Fi, GPS / GLONASS
Expansion slot microSD card

カラーはBlackで、HTCの本国である台湾製(Made in Taiwan)の記載もある。



本体および同梱品
ガイドブックらしきものが同梱されているが、全て英語表記となっており、筆者では歯が立たないのでスルーする。コンセントプラグとUSBケーブルが同梱されているが、コンセントプラグは日本で使えるものと形状が違うのでこれもスルー。ただし、渡航する際は別途用意しなくても持っていくと使えるので便利だろう(多分アメリカとかで使えるもののはず＝よくワカリマセン)。さらに、HTCのロゴが入ったイヤホンマイクも同梱する。 Beats Audio(ビーツ・オーディオ)のイヤホンでもなく、特に電話としても使わないのでこちらもスルーし、そっと箱の中にしまっておく。



本体正面（左）と背面（右）
本体サイズは幅59.7×高さ120.3×厚み9.2mm、重量は115g、ディスプレイは3.7インチのTFT液晶で解像度は480×800ドットとなる。コンパクトで軽量、片手で操作しやすく、手にも馴染みやすいサイズ。

CPUは1GHzのシングルコア（Qualcomm Scorpion）、GPUはQualcomm Adreno 205、ROMが4GB、RAMは512MBの本体メモリを搭載している。

Androidのバージョンは4.0.3(開発コード名：IceCream Sandwich；ICS)を採用し、独自UIのHTC Senseはバージョン4.0を搭載。スペック上はローエンドからミドルエンドユーザー向けと言えるモデルだ。



本体向かって左側面（画像上）と右側面（画像下）


本体向かって上部側面（画像上）と下部側面（画像下）
本体左側面にはmicroUSB端子を、右側面には上下キーを備える。本体上部側面には3.5mmのイヤホンジャックと電源キー、下部側面にはマイクを搭載している。



本体背面
国内で行った製品説明会ではブラウンが展示されていたため、ブラックの本体は初めて見たが想像を絶するカッコ良さだ。写真では伝わり難いのが残念。



背面のカメラ部分
背面のカメラは約500万画素のCMOS(裏面照射型)を搭載し、カメラモジュールの横にフォトライトを備える。画素数によるインパクトはないが、F値2.0という明るいレンズを搭載し、暗い場所でも明るく綺麗に撮影ができる。



背面の下部には Beats Audioのロゴとスピーカー


その部分のみがカバーとなっており外れる
背面下部のカバーを外すと、SIMスロットとmicroSDカードスロットが見える。microSDは最大32GBのmicroSDHCに対応し、SIMカードはmicroSIMではなく通常サイズのSIMカードが装着できる。

電池パックは内蔵タイプで、公式に発表されている電池パック容量は1500mAh。電池パックの交換できないが、フリーズした場合などは電源キーを長押下することで再起動ができる。



シャクレ！
デザイン面での最大の特長は、正面下部が手前にカーブを描いて出っ張っている(しゃくれている)部分だろう。筆者が持った際は小指が丁度このしゃくれた部分に乗り心地よく休めるため、勝手に“小指やすめ”と呼んでいるｗ

ディスプレイ直下にあるバック、ホーム、タスクキーを押す際もこの出っ張り部分があるため押しやすく、背面の質感もHTCならではのマットな仕上がり。SIMフリーモデルのためキャリア(通信事業者)のロゴも入っていない。



HTC One V First look

記事執筆：2106bpm（つとむびーぴーえむ）

■関連リンク
・エスマックス（S-MAX）
・エスマックス（S-MAX） smaxjp on Twitter
・HTCの新グローバル端末「HTC One」シリーズ3機種を実際に触ってみた「HTC One V編」【レポート】 - S-MAX - ライブドアブログ
・HTC Nippon、グローバルモデル「HTC One」シリーズの説明会を開催！日本への投入やKDDIとの協業については言及せず - S-MAX - ライブドアブログ
・HTC、Android 4.0 ICS搭載「HTC Oneシリーズ」を4機種発表！One X、One XL、One S、One Vが登場 - S-MAX - ライブドアブログ
・【最近のオススメ「Androidアプリ」特集：2012年6月4〜10日編】 - S-MAX - ライブドアブログ
・HTC One V Product Overview(HTC Corporation.)
・HTC 日本

===========
# 6841
http://news.livedoor.com/article/detail/6713879/
2012-07-02T12:55:00+0900
Meizu、クアッドコアCPU搭載Android 4.0 ICSスマートフォン「Meizu MX Quadcore」を香港で発売
ゼロから始めるスマートフォン 

中国メーカー「Meizu」は、クアッドコアCPUを搭載したスマートフォン「Meixu MX Quadcore」を2012年6月30日（土）に香港で発売開始しています。

当日販売は事前予約分のみということですが、売り場は入場制限がかかるほどのもの凄い人だかりができたそうです。

SoCは「GALAXY SIII」のグローバルモデルと同じサムスン電子製「Exynos 4412」を採用し、最大周波数1.4GHzのクアッドコアCPUを搭載しています。RAMは1GBで、ROMは32GBと64GBの2モデルが存在。かなりのハイスペック機種となります。OSはAndroid 4.0（開発コード名：IceCream Sandwich；ICS）をベースに独自にカスタマイズした「Flyme OS 1.0」を採用します。

その他、ディスプレイはシャープ製の4.0インチDoubleVGA（960×640）液晶、カメラは背面800万画素（裏面照射型CMOS）／前面30万画素、バッテリー容量は1,700mAhという構成。対応周波数は2G（GSM）：850／900／1800／1900、3G（WCDMA）：850／900／1700／1900／2100。端末サイズは121.3×63.3×10.3mm、重さは139gとなっています。

なお、情報元のショップ「KAIMONOTAI」では、販売および日本への発送も行なっています。価格は32GBモデルで38,300円、64GBモデルで48,300円。取り寄せ商品となり、入金確認後、6日〜7日後の発送になるということです。

記事執筆：ゼロから始めるスマートフォン

■ゼロから始めるスマートフォン
■中国MeizuがクアッドコアCPU搭載スマートフォン「Meizu MX Quadcore」を香港で発売 | ゼロから始めるスマートフォン

■関連リンク
・エスマックス（S-MAX）
・エスマックス（S-MAX） smaxjp on Twitter
・MEIZU
・Kaimonotai Blog ≫ Blog Archive ≫ Meizuの人気モデルMeizu MXにハイエンドのクアッドコア端末Meizu MX Quadcoreが登場。本日より香港にて一斉に発売開始 - すごい人だかりです.

===========
# 935
http://news.livedoor.com/article/detail/6781727/
2012-07-23T09:55:00+0900
HTC、「HTC Desire HD」へのAndroid 4.0 ICSアップデートを断念！パフォーマンス維持できない
ゼロから始めるスマートフォン 

HTCは、同社公式ブログ「HTC Blog — Inside Views & Breakthroughs from HTC」にて公開している同社製Androidスマートフォンに対するAndroid 4.0（開発コード名：IceCream Sandwich；ICS）へのOSバージョンアップ対象機種リストの中から「HTC Desire HD」を除外しています。

除外に際し、注釈にて「現在のAndroidバージョンおよびHTC Senseバージョンの状態が最も良いユーザー体験を与えられるということが、テストの結果わかった」と示し、Android 4.0へのアップデートを断念したことと、その理由を記しています。

After extensive testing, we’ve determined that the current version of HTC Sense with Android provides customers with the best experience on the HTC Desire HD. When we consider new versions of software, we weigh a number of factors, but ultimately the customer experience on the product is the deciding factor. We apologize for any confusion this change may have caused our customers.



HTC Desire HDは日本でもソフトバンクモバイルから「HTC Desire HD 001HT」として発売されています。CPUはシングルコアの1.0GHz（Qualcomm Snapdragon MSM8255）ながら、RAMサイズは768MBとなっており、同時期に発売された他メーカーの機種よりもスペック的には若干優れていました。

しかしながら、それでもAndroid 4.0では十分なパフォーマンスが得られず、最終的にアップデートされないという結果となってしまいました。非常に残念なところです。

記事執筆：ゼロから始めるスマートフォン

■ゼロから始めるスマートフォン
■HTC、「HTC Desire HD」へのAndroid4.0 ICSアップデートを断念、パフォーマンス維持できない | ゼロから始めるスマートフォン

■関連リンク
・エスマックス（S-MAX）
・エスマックス（S-MAX） smaxjp on Twitter
・Android 4.0, Ice Cream Sandwich Updates

===========

いずれも非常に近い内容の記事が表示されています。

ある記事のidを入力すればそれに近いニュース記事が類似度が近い順に出てくるのはまさにレコメンドです。

学習したモデル達を保存するのは以下のようにします。

d.save_as_text("dict.txt")
corpora.MmCorpus.serialize("cop.mm", corpus)
lda.save("lda.model")
doc_index.save("sim")

レコメンドを組み込みたいアプリケーションでロードする場合は以下のようします。

from gensim import models, corpora, similarities

corpus = corpora.MmCorpus("cop.mm")
lda = models.ldamodel.LdaModel.load("lda.model")
d = corpora.Dictionary.load_from_text("dict.txt")
doc_index = similarities.docsim.MatrixSimilarity.load("sim")

ニュース記事レコメンドを作る事が出来ました！！

終わりに

こんなに簡単にニュース記事レコメンドが出来るとは良い時代じゃな。
notebookはここに置いてます。
github.com

ツイッターやっているのでフォローお願いします！！

↓今すぐフォローすべきキラキラアカウント

Follow @tdualdir

じゃあの。

参考書

*1:Bag of Words 　多重集合（Bag）とは重複を許した集合　また、Bag of Wordsで表現することは単語の並び順は考慮せずに単語の出現率だけに注力する事を意味している。

*2:D. M. Blei, A. Y. Ng, and M. I. Jordan. Latent Dirichlet allocation.

*3:Kroneckerのデルタ ${\displaystyle \delta_{ij} = \begin{cases} 1 & (i=j) \\ 0 & (i \neq j ) \end{cases} }$

*4:単体（simplex) 　n+1個の位置ベクトル $({\bf v}_1,{\bf v}_2,...,{\bf v}_{n+1})$ があり、それらの点がどの部分空間にも含まれない時に　 $\phi_i$ は実数で $\sum_{i=1}^{n+1}\phi_i=1$ かつ $\phi_1,\phi_2,...,\phi_{n+1} \geq 0$ を満たす $\sum_{i=1}^{n+1}\phi_{i}{\bf v}_{i}$ をn次元単体（simplex）という。　0次元が点,１次元が線,２次元が三角形,3次元が四面体というように図形を分割した時の最小単位を表現しており、位相幾何学などでも使われる概念。　Dirichlet分布やカテゴリカル分布は単体を作っている。

*5:崩壊型ギブスサンプリングなど

*6:log関数はアンダーフロー防止が出来て単調増加で滑らかな凸関数なので都合が良い。

*7:Jensenの不等式とは　f(x)が上に凸で、 $\int p(x) dx = 1$ の時、次の不等式が成り立つ　 $f\left( \int y(x)p(x) dx \right) \ge \int f\left(y(x) \right)p(x) dx$

*8:　Kullback–Leibler divergenceは確率分布の類似度。　xが連続変数の時, $D_{KL}\left(q(x)\mid p(x) \right)= \int q(x)\log \frac{q(x)}{p(x)}dx$ 　xが離散変数の時, $D_{KL}\left(q(x)\mid p(x) \right)= \sum_x q(x)\log \frac{q(x)}{p(x)}$ 　 $q(x)$ と $p(x)$ が同じ分布である必要十分条件はKL divergenceが0

*9:汎関数のちゃんとした定義はベクトル空間から体への写像です。

*10:Euler-Lagrange方程式　汎関数を $I\left(x(t),\dot{x}(t) \right) = \int L \left(x(t),\dot{x}(t) \right) dt$ とした時、（但し、 $\dot{x}(t) = \frac{dx(t)}{dt}$ ） ${\displaystyle \frac{d}{dt}\frac{\partial L}{\partial \dot{x}(t)} -\frac{\partial L}{\partial x(t)} = 0 }$ 　（詳細や導出などはPRMLにあった気がする。）